这一章将主要介绍使用3×33 \times 3矩阵进行三维孔径啊下的线性变化（Linear Transformations）。线性变化是不包含位移的，包含了位移的变换称为仿射变换（Affine Transformation）。三维中的仿射变换不能使用3×33 \times 3矩阵来实现。

5.1 旋转

5.1.1 在二维中的旋转

在二维空间中的旋转是基于一个点的。对于基于原点的二维旋转，只有一个变量即旋转角度θ\theta，而且通常而言顺时针旋转为正方向，逆时针旋转为反方向。下图中基向量p\mathbf{p}和q\mathbf{q}如何围绕原点旋转，从而产生新的基向量p′\mathbf{p^{'}}和q′\mathbf{q^{'}}。

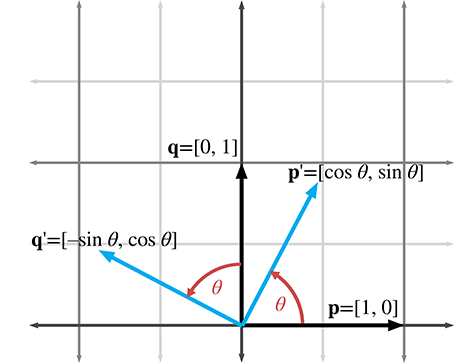
在二维中围绕原点旋转

二维旋转矩阵如下：

R(θ)=[p′q′][cos⁡θsin⁡θ−sin⁡θcos⁡θ]\mathbf{R}(\theta)= \begin{bmatrix} \quad \mathbf{p^{'}} \quad \\ \quad \mathbf{q^{'}} \quad \end{bmatrix} \begin{bmatrix}\cos{\theta}&\sin{\theta}\\-\sin{\theta}&\cos{\theta} \end{bmatrix}

5.1.2 围绕主轴的三维旋转

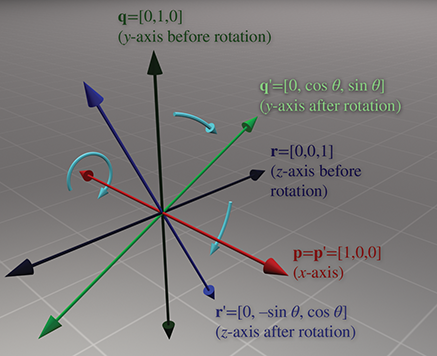
在三维中，旋转发生在一个轴而不是一个点上，术语轴（Axis）呈现它更常见的定义：它是一条线。旋转并不一定是基本x，y或z轴之一。以下是基于三个基向量轴的旋转：

  • 围绕x轴旋转的三维矩阵：

Rx(θ)=[p′q′r′][1000cos⁡θsin⁡θ0−sin⁡θcos⁡θ]\mathbf{R}_x(\theta)= \begin{bmatrix} \quad \mathbf{p^{'}} \quad \\ \quad \mathbf{q^{'}} \quad \\ \quad \mathbf{r^{'}} \quad \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\theta} & \sin{\theta}\\ 0 & -\sin{\theta} & \cos{\theta} \end{bmatrix}

  • 围绕y轴旋转的三维矩阵：

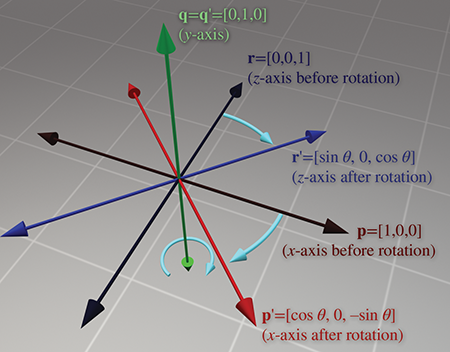
Ry(θ)=[p′q′r′][cos⁡θ0−sin⁡θ010sin⁡θ0cos⁡θ]\mathbf{R}_y(\theta)= \begin{bmatrix} \quad \mathbf{p^{'}} \quad \\ \quad \mathbf{q^{'}} \quad \\ \quad \mathbf{r^{'}} \quad \end{bmatrix} \begin{bmatrix} \cos{\theta} & 0 & -\sin{\theta} \\ 0 & 1 & 0 \\ \sin{\theta} & 0 & \cos{\theta} \end{bmatrix}

  • 围绕z轴旋转的三维矩阵：

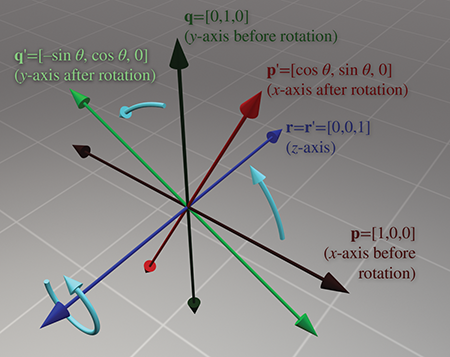
Rz(θ)=[p′q′r′][cos⁡θsin⁡θ0−sin⁡θcos⁡θ0001]\mathbf{R}_z(\theta)= \begin{bmatrix} \quad \mathbf{p^{'}} \quad \\ \quad \mathbf{q^{'}} \quad \\ \quad \mathbf{r^{'}} \quad \end{bmatrix} \begin{bmatrix} \cos{\theta} & \sin{\theta} & 0 \\ -\sin{\theta} & \cos{\theta} & 0 \\ 0 & 0 & 1 \end{bmatrix}

下图依次从左往右是围绕x，y，z轴旋转示意图。

在三维中围绕x轴旋转
在三维中围绕y轴旋转
在三维中围绕z轴旋转

5.1.3 围绕任意轴的三维旋转

我们将θ\theta定义为绕轴的旋转量，轴将由n^\mathbf{\hat{n}}定义。我们将需要推导出矩阵R(n^,θ)\mathbf{R}(\mathbf{\hat{n}, \theta})，使得将向量v\mathbf{v}乘以R(n^,θ)\mathbf{R}(\mathbf{\hat{n}, \theta})时，得到向量v′\mathbf{v^{'}}是将v\mathbf{v}旋转角度θ\theta的以下结果：

v′=vR(n^,θ)\mathbf{v^{'}} = \mathbf{v}\mathbf{R}(\mathbf{\hat{n}, \theta})

推到过程如下：

  1. 为了计算方便，基本思路是解决垂直于v′\mathbf{v^{'}}的平面中的问题，这是一个更简单的二维问题。所以我们将v\mathbf{v}拆分为两个向量v∣∣\mathbf{v_{||}}和v⊥\mathbf{v_{\bot}}，它们分别平行和垂直于n^\mathbf{\hat{n}}，使得v=v∣∣+v⊥\mathbf{v}=\mathbf{v_{||}}+\mathbf{v_{\bot}}。通过单独旋转每个分量，可以将向量作为一个整体旋转。换句话来说v′=v∣∣′+v⊥′\mathbf{v}^{'}=\mathbf{v_{||}}^{'}+\mathbf{v_{\bot}}^{'}。由于v∣∣\mathbf{v_{||}}于n^\mathbf{\hat{n}}平行，因此它不会受到围绕n^\mathbf{\hat{n}}旋转的影响。换句话来说v∣∣′=v∣∣\mathbf{v}_{||}^{'}=\mathbf{v}_{||}。所以需要做的就是计算v⊥′\mathbf{v}_{\bot}^{'}，然后得到v′=v∣∣+v⊥′\mathbf{v}^{'}=\mathbf{v}_{||}+\mathbf{v}_{\bot}^{'}，可以构造向量v∣∣、v⊥\mathbf{v}_{||}、\mathbf{v}_{\bot}和中间向量w\mathbf{w}，如下图所示:
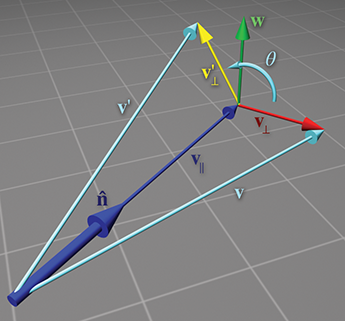
    围绕任意轴旋转向量

  2. 向量v∣∣\mathbf{v}_{||}是v\mathbf{v}的与n^\mathbf{\hat{n}}平行的部分（v∣∣\mathbf{v}_{||}是投影到n^\mathbf{\hat{n}}上的v\mathbf{v}的值），则有v∣∣=(v⋅n^)n^\mathbf{v}_{||}=\mathbf{(v\cdot\hat{n})\hat{n}}。

  3. 向量v⊥\mathbf{v}_{\bot}是v\mathbf{v}的与n^\mathbf{\hat{n}}垂直的部分（v⊥\mathbf{v}_{\bot}是将v\mathbf{v}投影到垂直于n^\mathbf{\hat{n}}的平面上的结果），由于v=v∣∣+v⊥\mathbf{v=v_{||}+v_{\bot}},则有v⊥=v−v∣∣\mathbf{v_{\bot}=v - v_{||}}。

  4. 向量w\mathbf{w}是为了与向量v⊥\mathbf{v}_{\bot}构成一个平面。向量w\mathbf{w}垂直于v∣∣\mathbf{v}_{||}和v⊥\mathbf{v}_{\bot}，并且长度与v⊥\mathbf{v}_{\bot}相同。w\mathbf{w}可以通过围绕n^\mathbf{\hat{n}}旋转v⊥\mathbf{v}_{\bot}为90∘90^{\circ}来构造。则有w=n^×v⊥\mathbf{w=\hat{n}\times v_{\bot}}。

  5. 此时,w\mathbf{w}和v⊥\mathbf{v}_{\bot}构成了一个二维平面，使用作v⊥\mathbf{v}_{\bot}和w\mathbf{w}为基向量，根据线条旋转（第1.4.4章节中的单位线条旋转）可得:v⊥′=cos⁡θv⊥+sin⁡θw\mathbf{v}_{\bot}^{'}=\cos\theta\mathbf{v}_{\bot}+\sin{\theta}\mathbf{w}。

  6. 总结一下就能得出以下向量：

v∣∣=(v⋅n^)n^,v⊥=v−v∣∣=v−(v⋅n^)n^,w=n^×v⊥=n^×(v−v∣∣)=n^×v−n^×v∣∣=n^×v−0=n^×v,v⊥′=cos⁡θv⊥+sin⁡θw=cos⁡θ(v−(v⋅n^)n^)+sin⁡θ(n^×v)v′=v⊥′+v∣∣=cos⁡θ(v−(v⋅n^)n^)+sin⁡θ(n^×v)+(v⋅n^)n^\begin{align} \mathbf{v}_{||} &= \mathbf{(v\cdot\hat{n})\hat{n}}, \\ \mathbf{v}_{\bot} &= \mathbf{v-v_{||}}=\mathbf{v-(v\cdot\hat{n})\hat{n}}, \\ \mathbf{w} &= \mathbf{\hat{n}\times v_{\bot}} \\ &= \mathbf{\hat{n}\times(v-v_{||})} \\ &= \mathbf{\hat{n}\times v - \hat{n}\times v_{||}} \\ &= \mathbf{\hat{n}\times v - 0} \\ &= \mathbf{\hat{n}\times v}, \\ \mathbf{v}_{\bot}^{'} &= \cos{\theta}\mathbf{v}_{\bot}+\sin{\theta}\mathbf{w} \\ &= \cos{\theta}(\mathbf{v - (v\cdot\hat{n})\hat{n}})+\sin{\theta}(\mathbf{\hat{n}\times v}) \\ \mathbf{v}^{'} &= \mathbf{v_{\bot}^{'} + v_{||}} \\ &= \cos{\theta}(\mathbf{v - (v\cdot\hat{n})\hat{n}})+\sin{\theta}(\mathbf{\hat{n}\times v}) + \mathbf{(v\cdot\hat{n})\hat{n}} \end{align}

  1. 现在已经用v、n^\mathbf{v、\hat{n}}和θ\theta来表示v′\mathbf{v}_{'}，接下来计算转换后的基向量：
  • 有p=[100],n^=[nxnynz],\mathbf{p}=\begin{bmatrix}1&0&0\end{bmatrix},\mathbf{\hat{n}}=\begin{bmatrix}n_x&n_y&n_z\end{bmatrix},则

p′=cos⁡θ(p−(p⋅n^)n^)+sin⁡θ(n^×p)+(p⋅n^)n^=((cos⁡θ(p−(p⋅n^)n^)+sin⁡θ(n^×p)+(p⋅n^)n^)T)T=(cos⁡θ(pT−(pT⋅n^T)n^T)+sin⁡θ(n^T×pT)+(pT⋅n^T)n^T)T=(cos⁡θ([100]−[100]⋅[nxnynz])+sin⁡θ([nxnynz]×[100])+([100]⋅[nxnynz])[nxnynz])T=(cos⁡θ([100]−nx[nxnynz])+sin⁡θ[0nz−ny]+nx[nxnynz])T=(cos⁡θ[1−nx2−nxny−nxnz]+sin⁡θ[0nz−ny]+[nx2nxnynxnz])T=([cos⁡θ−nx2cos⁡θ−nxnycos⁡θ−nxnzcos⁡θ]+[0nzsin⁡θ−nysin⁡θ]+[nx2nxnynxnz])T=[cos⁡θ−nx2cos⁡θ+nx2−nxnycos⁡θ+nzsin⁡θ+nxny−nxnzcos⁡θ−nysin⁡θ+nxnz]T=[nx2(1−cos⁡θ)+cos⁡θnxny(1−cos⁡θ)+nzsin⁡θnxnz(1−cos⁡θ)+nysin⁡θ]T=[nx2(1−cos⁡θ)+cos⁡θnxny(1−cos⁡θ)+nzsin⁡θnxnz(1−cos⁡θ)+nysin⁡θ]\begin{align} \mathbf{p}^{'} &= \cos{\theta}\mathbf{(p - (p\cdot \hat{n})\hat{n})}+\sin{\theta}(\mathbf{\hat{n}\times p})+\mathbf{(p\cdot \hat{n})\hat{n}} \\ &= ((\cos{\theta}\mathbf{(p - (p\cdot \hat{n})\hat{n})}+\sin{\theta}(\mathbf{\hat{n}\times p})+\mathbf{(p\cdot \hat{n})\hat{n}})^T)^T \\ &= (\cos{\theta}(\mathbf{p^T - (p^T\cdot\hat{n}^T)\hat{n}^T})+\sin{\theta}(\mathbf{\hat{n}^T\times p^T)}+\mathbf{(p^T\cdot\hat{n}^T)\hat{n}^T})^T \\ &= (\cos{\theta}(\begin{bmatrix}1\\0\\0\end{bmatrix}-\begin{bmatrix}1\\0\\0\end{bmatrix}\cdot\begin{bmatrix}n_x\\n_y\\n_z\end{bmatrix}) + \sin{\theta}(\begin{bmatrix}n_x\\n_y\\n_z\end{bmatrix} \times \begin{bmatrix}1\\0\\0\end{bmatrix}) + (\begin{bmatrix}1\\0\\0\end{bmatrix} \cdot \begin{bmatrix}n_x\\n_y\\n_z\end{bmatrix})\begin{bmatrix}n_x\\n_y\\n_z\end{bmatrix} )^T \\ &= (\cos{\theta}(\begin{bmatrix}1\\0\\0\end{bmatrix} - n_x\begin{bmatrix}n_x\\n_y\\n_z\end{bmatrix})+\sin{\theta}\begin{bmatrix}0\\n_z\\-n_y\end{bmatrix} + n_x\begin{bmatrix}n_x\\n_y\\n_z\end{bmatrix} )^T \\ &= (\cos{\theta}\begin{bmatrix}{1-n_x^2}\\{-n_xn_y}\\{-n_xn_z}\end{bmatrix} + \sin{\theta}\begin{bmatrix}0\\n_z\\-n_y\end{bmatrix} + \begin{bmatrix}n_x^2\\n_xn_y\\n_xn_z\end{bmatrix} )^T \\ &= ( \begin{bmatrix}{\cos{\theta} - n_x^2\cos{\theta}} \\ {-n_xn_y\cos{\theta}} \\ {-n_xn_z\cos{\theta}} \end{bmatrix} + \begin{bmatrix}0\\{n_z\sin{\theta}}\\{-n_y\sin{\theta}}\end{bmatrix} + \begin{bmatrix}n_x^2\\n_xn_y\\n_xn_z\end{bmatrix} )^T \\ &= \begin{bmatrix} \cos\theta-n_x^2\cos\theta+n_x^2 \\ -n_xn_y\cos\theta+n_z\sin\theta+n_xn_y \\ -n_xn_z\cos\theta-n_y\sin\theta+n_xn_z \end{bmatrix}^T \\ &= \begin{bmatrix} n_x^2(1-\cos\theta)+\cos\theta \\ n_xn_y(1-\cos\theta) + n_z\sin\theta \\ n_xn_z(1-\cos\theta) + n_y\sin\theta \end{bmatrix}^T \\ &= \begin{bmatrix} n_x^2(1-\cos\theta)+\cos\theta & n_xn_y(1-\cos\theta) + n_z\sin\theta & n_xn_z(1-\cos\theta) + n_y\sin\theta \end{bmatrix} \end{align}

  • 有q=[010],n^=[nxnynz],\mathbf{q}=\begin{bmatrix}0&1&0\end{bmatrix}, \mathbf{\hat{n}}=\begin{bmatrix}n_x&n_y&n_z\end{bmatrix},则

q′=[nxny(1−cos⁡θ)−nzsin⁡θny2(1−cos⁡θ)+cos⁡θnynz(1−cos⁡θ)+nxsin⁡θ]T\mathbf{q}^{'} = \begin{bmatrix} n_xn_y(1-\cos\theta) - n_z\sin\theta \\ n_y^2(1-\cos\theta)+\cos\theta \\ n_yn_z(1-\cos\theta) + n_x\sin\theta \end{bmatrix}^T

  • 有r=[001],n^=[nxnynz],\mathbf{r}=\begin{bmatrix}0&0&1\end{bmatrix}, \mathbf{\hat{n}}=\begin{bmatrix}n_x&n_y&n_z\end{bmatrix},则

r′=[nxnz(1−cos⁡θ)+nysin⁡θnynz(1−cos⁡θ)−nxsin⁡θnz2(1−cos⁡θ)+cos⁡θ]T\mathbf{r}^{'} = \begin{bmatrix} n_xn_z(1-\cos\theta) + n_y\sin\theta \\ n_yn_z(1-\cos\theta) -n_x\sin\theta \\ n_z^2(1-\cos\theta) + \cos\theta \end{bmatrix}^T

  1. p′、q′\mathbf{p^{'}、q^{'}}和r′\mathbf{r}^{'}实际是行向量，也是基向量，我们用他们构造旋转矩阵可得：

R(n^,θ)=[p′q′r′]=[nx2(1−cos⁡θ)+cos⁡θnxny(1−cos⁡θ)+nzsin⁡θnxnz(1−cos⁡θ)+nysin⁡θnxny(1−cos⁡θ)−nzsin⁡θny2(1−cos⁡θ)+cos⁡θnynz(1−cos⁡θ)+nxsin⁡θnxnz(1−cos⁡θ)+nysin⁡θnynz(1−cos⁡θ)−nxsin⁡θnz2(1−cos⁡θ)+cos⁡θ]\mathbf{R}(\mathbf{\hat{n}, \theta})= \begin{bmatrix} \quad \mathbf{p^{'}} \quad \\ \quad \mathbf{q^{'}} \quad \\ \quad \mathbf{r^{'}} \quad \end{bmatrix} = \begin{bmatrix} n_x^2(1-\cos\theta)+\cos\theta & n_xn_y(1-\cos\theta) + n_z\sin\theta & n_xn_z(1-\cos\theta) + n_y\sin\theta \\ n_xn_y(1-\cos\theta) - n_z\sin\theta & n_y^2(1-\cos\theta)+\cos\theta & n_yn_z(1-\cos\theta) + n_x\sin\theta \\ n_xn_z(1-\cos\theta) + n_y\sin\theta & n_yn_z(1-\cos\theta) -n_x\sin\theta & n_z^2(1-\cos\theta) + \cos\theta \end{bmatrix}

5.2 缩放

缩放一个对象，使其按比例增大或缩小一个k的因子，如果所有轴的比例因子相等，则执行均匀缩放（Uniform Scale），反之为不均匀缩放。

  • 如果|k|<1,则对象在这个方向上变得“更短”。
  • 如果|k|>1,则对象在这个方向上变得“更长”。
  • 如果k=0，那么将获得一个正交投影（Orthographic Projection）。
  • 如果k<0，那么将获得一个反射的结果。

5.2.1 沿主轴缩放

最简单的缩放操作是沿每个轴应用单独的比例因子。

使用和的各种不同比例因子缩放一个二维对象

从直观上看，基向量p\mathbf{p}和q\mathbf{q}独立地受相应的比例因子的影响，如下表示：

p′=kxp=kx[10]=[kx0]q′=kyq=ky[01]=[0ky]\mathbf{p}^{'} = k_x\mathbf{p} = k_x\begin{bmatrix}1&0\end{bmatrix}=\begin{bmatrix}k_x&0\end{bmatrix} \\ \mathbf{q}^{'} = k_y\mathbf{q} = k_y\begin{bmatrix}0&1\end{bmatrix}=\begin{bmatrix}0&k_y\end{bmatrix}

用这些基向量构造二维缩放矩阵S(kx,ky)\mathbf{S}(k_x,k_y)，可得围绕主轴缩放的二维矩阵如下表述：

S(kx,ky)=[p′q′]=[kx00ky]\mathbf{S}(k_x,k_y)=\begin{bmatrix}\mathbf{p}^{'} \\ \mathbf{q}^{'}\end{bmatrix}=\begin{bmatrix}k_x&0\\0&k_y\end{bmatrix}

而对于三维来说，添加第三个比例因子kzk_z，得到如下围绕主轴的三维缩放矩阵：

S(kx,ky,kz)=[p′q′r′]=[kx000ky000kz]\mathbf{S}(k_x,k_y,k_z)= \begin{bmatrix}\mathbf{p}^{'} \\ \mathbf{q}^{'}\\ \mathbf{r}^{'} \end{bmatrix} =\begin{bmatrix}k_x&0&0\\0&k_y&0\\0&0&k_z\end{bmatrix}

如果任意向量乘以上述的三维矩阵，那么我们的每个分量都将按适当的比例因子缩放,表述如下：

[xyz]=[kx000ky000kz]=[kxxkyykzz]\begin{bmatrix}x&y&z\end{bmatrix} =\begin{bmatrix}k_x&0&0\\0&k_y&0\\0&0&k_z\end{bmatrix} =\begin{bmatrix}k_xx&k_yy&k_zz\end{bmatrix}

5.2.2 任意方向的缩放

将n^\mathbf{\hat{n}}定义为平行于缩放方向的单位向量，给定任意向量v\mathbf{v}，计算沿着n^缩放后的\mathbf{\hat{n}}缩放后的v′\mathbf{v}^{'}。

推导如下：

  1. 将v\mathbf{v}拆分为两个向量v∣∣\mathbf{v_{||}}和v⊥\mathbf{v_{\bot}},它们分别平行和垂直于n^\mathbf{\hat{n}},使得v=v∣∣+v⊥\mathbf{v}=\mathbf{v_{||}}+\mathbf{v_{\bot}}。平行部分v∣∣\mathbf{v}_{||}是v\mathbf{v}在n^\mathbf{\hat{n}}上的投影，则有v∣∣=(v⋅n^)n^\mathbf{v_{||}=(v\cdot\hat{n})\hat{n}}。由于v⊥\mathbf{v}_{\bot}垂直于n^\mathbf{\hat{n}} ，它不受缩放操作的影响，因此v′=v∣∣′+v⊥′\mathbf{v}^{'}=\mathbf{v_{||}}^{'}+\mathbf{v_{\bot}}^{'}。

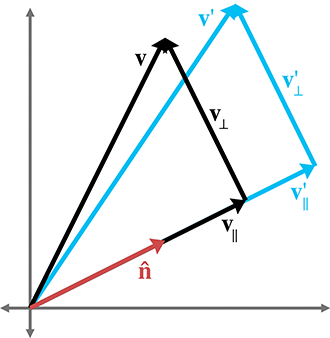
沿任意方向缩放向量

  1. 由于v∣∣\mathbf{v}_{||}平行于缩放方向，因此v∣∣′=kv∣∣\mathbf{v}_{||}^{'}=k\mathbf{v}_{||}。代入后则有：

v=v∣∣+v⊥,v∣∣=(v⋅n^)n^v⊥′=v⊥=v−v∣∣=v−(v⋅n^)n^,v∣∣′=kv∣∣=k(v⋅n^)n^,\begin{align} \mathbf{v} &= \mathbf{v_{||}}+\mathbf{v_{\bot}}, \\ \mathbf{v_{||}} &= \mathbf{(v\cdot\hat{n})\hat{n}} \\ \mathbf{v_{\bot}^{'}} &= \mathbf{v_{\bot}} \\ &= \mathbf{v-v_{||}} \\ &= \mathbf{v-(v\cdot\hat{n})\hat{n}}, \\ \mathbf{v_{||}^{'}} &= k\mathbf{v_{||}} \\ &= k\mathbf{(v\cdot\hat{n})\hat{n}}, \\ \end{align}

  1. 则可以求得v′\mathbf{v^{'}}：

v′=v⊥′+v∣∣′=v−(v⋅n^)n^+k(v⋅n^)n^=v+(k−1)(v⋅n^)n^\begin{align} \mathbf{v^{'}} &= \mathbf{v_{\bot}^{'}}+\mathbf{v_{||}^{'}} \\ &= \mathbf{v-(v\cdot \hat{n})\hat{n}} + k\mathbf{(v\cdot \hat{n})\hat{n}} \\ &= \mathbf{v}+(k-1)\mathbf{(v\cdot \hat{n})\hat{n}} \end{align}

  1. 现在我们可以获得缩放矩阵的几个基向量了：
  • 有p=[100],n^=[nxnynz],\mathbf{p}=\begin{bmatrix}1&0&0\end{bmatrix},\mathbf{\hat{n}}=\begin{bmatrix}n_x&n_y&n_z\end{bmatrix},则

p′=p+(k−1)(p⋅n^)n^=((p+(k−1)(p⋅n^)n^)T)T=(pT+(k−1)(pT⋅n^T)n^T)T=([100]+(k−1)([100]⋅[nxnynz])[nxnynz])T=([100]+(k−1)(nx[nxnynz]))T=([100]+[(k−1)nx2(k−1)nxny(k−1)nxnz])T=[1+(k−1)nx2(k−1)nxny(k−1)nxnz]T=[1+(k−1)nx2(k−1)nxny(k−1)nxnz]\begin{align} \mathbf{p^{'}} &= \mathbf{p}+(k-1)\mathbf{(p\cdot \hat{n})\hat{n}} \\ &= ((\mathbf{p}+(k-1)\mathbf{(p\cdot \hat{n})\hat{n}})^T)^T \\ &= (\mathbf{p^T}+(k-1)\mathbf{(p^T\cdot \hat{n}^T)\hat{n}}^T)^T \\ &= (\begin{bmatrix}1\\0\\0\end{bmatrix}+(k-1)(\begin{bmatrix}1\\0\\0\end{bmatrix}\cdot\begin{bmatrix}n_x\\n_y\\n_z\end{bmatrix})\begin{bmatrix}n_x\\n_y\\n_z\end{bmatrix})^T \\ &= (\begin{bmatrix}1\\0\\0\end{bmatrix}+(k-1)(n_x\begin{bmatrix}n_x\\n_y\\n_z\end{bmatrix}) )^T \\ &= (\begin{bmatrix}1\\0\\0\end{bmatrix} + \begin{bmatrix}(k-1)n_x^2\\(k-1)n_xn_y\\(k-1)n_xn_z\end{bmatrix})^T \\ &= \begin{bmatrix}1+(k-1)n_x^2 \\ (k-1)n_xn_y \\ (k-1)n_xn_z \end{bmatrix}^T \\ &= \begin{bmatrix}1+(k-1)n_x^2 & (k-1)n_xn_y & (k-1)n_xn_z \end{bmatrix} \end{align}

  • 有q=[010],n^=[nxnynz],\mathbf{q}=\begin{bmatrix}0&1&0\end{bmatrix},\mathbf{\hat{n}}=\begin{bmatrix}n_x&n_y&n_z\end{bmatrix},则

q′=[(k−1)nxny1+(k−1)ny2(k−1)nynz]T\mathbf{q^{'}} =\begin{bmatrix}(k-1)n_xn_y\\1+(k-1)n_y^2\\(k-1)n_yn_z\end{bmatrix}^T

  • 有r=[001],n^=[nxnynz],\mathbf{r}=\begin{bmatrix}0&0&1\end{bmatrix},\mathbf{\hat{n}}=\begin{bmatrix}n_x&n_y&n_z\end{bmatrix},则

r′=[(k−1)nxnz(k−1)nynz1+(k−1)nz2]T\mathbf{r^{'}} =\begin{bmatrix}(k-1)n_xn_z\\(k-1)n_yn_z\\1+(k-1)n_z^2\end{bmatrix}^T

  1. p′、q′\mathbf{p^{'}、q^{'}}和r′\mathbf{r}^{'}实际是行向量，也是基向量，我们用他们构造缩放矩阵可得：

S(n^,k)=[p′q′r′]=[1+(k−1)nx2(k−1)nxny(k−1)nxnz(k−1)nxny1+(k−1)ny2(k−1)nynz(k−1)nxnz(k−1)nynz1+(k−1)nz2]\mathbf{S}(\mathbf{\hat{n}}, k)= \begin{bmatrix} \quad \mathbf{p^{'}} \quad \\ \quad \mathbf{q^{'}} \quad \\ \quad \mathbf{r^{'}} \quad \end{bmatrix} = \begin{bmatrix} 1+(k-1)n_x^2 & (k-1)n_xn_y & (k-1)n_xn_z \\ (k-1)n_xn_y & 1+(k-1)n_y^2 & (k-1)n_yn_z \\ (k-1)n_xn_z & (k-1)n_yn_z & 1+(k-1)n_z^2 \end{bmatrix}

5.3 正交投影

术语投影（Projection）指的是任何降维操作。实现投影的一种方法是在一个方向上使用零比例因子。这种所有点被扁平化或投影到垂直轴或平面上。这种类型的投影叫做正交投影（Orthographic Projection），也称为平行投影（Parallel Projection）。

5.3.1 投影到主轴或主平面上

我们通过垂直轴上使用零刻度值投影到主轴或主平面上。

将三维对象投影到主平面上

如果投影到xyxy平面上，那么即沿着zz轴缩放到0。即将n^=[001]\mathbf{\hat{n}}=\begin{bmatrix}0&0&1\end{bmatrix}，k=0k=0，代入到缩放矩阵中，则有：

S(n^,k)=[1+(k−1)nx2(k−1)nxny(k−1)nxnz(k−1)nxny1+(k−1)ny2(k−1)nynz(k−1)nxnz(k−1)nynz1+(k−1)nz2]Pxy=S([001],0)=[100010000]\mathbf{S}(\mathbf{\hat{n}}, k)= \begin{bmatrix} 1+(k-1)n_x^2 & (k-1)n_xn_y & (k-1)n_xn_z \\ (k-1)n_xn_y & 1+(k-1)n_y^2 & (k-1)n_yn_z \\ (k-1)n_xn_z & (k-1)n_yn_z & 1+(k-1)n_z^2 \end{bmatrix} \\ \mathbf{P}_{xy} = \mathbf{S}(\begin{bmatrix}0&0&1\end{bmatrix}, 0)=\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix} \\

同理，可获得：

Pxz=S([010],0)=[100000001]Pyz=S([100],0)=[000010001]\begin{align} \mathbf{P}_{xz} &= \mathbf{S}(\begin{bmatrix}0&1&0\end{bmatrix}, 0)=\begin{bmatrix}1&0&0\\0&0&0\\0&0&1\end{bmatrix} \\ \mathbf{P}_{yz} &= \mathbf{S}(\begin{bmatrix}1&0&0\end{bmatrix}, 0)=\begin{bmatrix}0&0&0\\0&1&0\\0&0&1\end{bmatrix} \end{align}

5.3.2 投影到任意线或平面上

如果投影到任意平面上，且向量n^\mathbf{\hat{n}}垂直于该平面。那么投影实际上是相当于沿着向量n^\mathbf{\hat{n}}进行缩放，且缩放系数k=0k=0。将其代入沿着任意角度进行缩放的矩阵，即

R(n^)=S(n^,0)=[1+(0−1)nx2(0−1)nxny(0−1)nxnz(0−1)nxny1+(0−1)ny2(0−1)nynz(0−1)nxnz(0−1)nynz1+(0−1)nz2]=[1−nx2−nxny−nxnz−nxny1−ny2−nynz−nxnz−nynz1−nz2]R(\mathbf{\hat{n}})=\mathbf{S}(\mathbf{\hat{n}}, 0)= \begin{bmatrix} 1+(0-1)n_x^2 & (0-1)n_xn_y & (0-1)n_xn_z \\ (0-1)n_xn_y & 1+(0-1)n_y^2 & (0-1)n_yn_z \\ (0-1)n_xn_z & (0-1)n_yn_z & 1+(0-1)n_z^2 \end{bmatrix} = \begin{bmatrix} 1-n_x^2 & -n_xn_y & -n_xn_z \\ -n_xn_y & 1-n_y^2 & -n_yn_z \\ -n_xn_z & -n_yn_z & 1-n_z^2 \end{bmatrix}

5.4 反射

反射（Reflection）也称为镜像（Mirroring），是一种围绕直线（在二维中）或平面（在三维中）“翻转”对象的变换。围绕二维中的轴反射对象如下图所示：

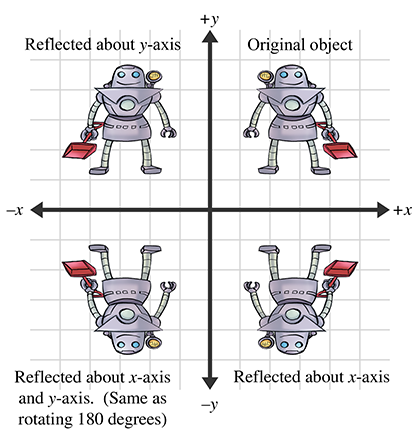
围绕二维中的轴反射对象

我们可以使用缩放的比例因子为-1来完成反射，即k=−1k=-1,则有围绕任意轴的反射矩阵如下所述：

R(n^)=S(n^,−1)=[1+(−1−1)nx2(−1−1)nxny(−1−1)nxnz(−1−1)nxny1+(−1−1)ny2(−1−1)nynz(−1−1)nxnz(−1−1)nynz1+(−1−1)nz2]=[1−2nx2−2nxny−2nxnz−2nxny1−2ny2−2nynz−2nxnz−2nynz1−2nz2]R(\mathbf{\hat{n}})=\mathbf{S}(\mathbf{\hat{n}}, -1)= \begin{bmatrix} 1+(-1-1)n_x^2 & (-1-1)n_xn_y & (-1-1)n_xn_z \\ (-1-1)n_xn_y & 1+(-1-1)n_y^2 & (-1-1)n_yn_z \\ (-1-1)n_xn_z & (-1-1)n_yn_z & 1+(-1-1)n_z^2 \end{bmatrix} = \begin{bmatrix} 1-2n_x^2 & -2n_xn_y & -2n_xn_z \\ -2n_xn_y & 1-2n_y^2 & -2n_yn_z \\ -2n_xn_z & -2n_yn_z & 1-2n_z^2 \end{bmatrix}

注意：对象智能“反射”一次。再次反射它时，那么对象将被翻转回“右侧朝外”。

5.5 错切

错切/切变（Shearing）是一种"倾斜"坐标空间的变形，它将不均匀地拉伸坐标空间，不保留角度，但面积会保留。错切是一种很少使用的变换，它也被称为倾斜变形（Skew Transform）。基本思路是将一个坐标的倍数加到另一个坐标上。

如x′=x+sy\mathbf{x}^{'}=x+sy，对应的矩阵为：

Hx(s)=[10s1]\mathbf{H_x}(s)=\begin{bmatrix}1&0\\s&1\end{bmatrix}

矩阵中的ss即对应计算过程0+s×10+s \times 1。从矩阵可以看出基本向量[10]\begin{bmatrix}1&0\end{bmatrix}并没有发生变化，基本向量[01]\begin{bmatrix}0&1\end{bmatrix}变为了[s1]\begin{bmatrix}s&1\end{bmatrix}。

Hx(s)\mathbf{H_x}(s)表示x被y轴切变，即x轴的值受y轴的影响，如下图中所示：

在二维中的错切

同理，如果在三维坐标中，Hxy\mathbf{H_{xy}}表示xy平面被z轴坐标影响。所有的三维空间切变矩阵如下所示：

Hxy(s,t)=[100010st1]Hxz(s,t)=[100s1t001]Hyz(s,t)=[1st010001]\begin{align} \mathbf{H}_{xy}(s,t) &= \begin{bmatrix}1&0&0\\0&1&0\\s&t&1\end{bmatrix} \\ \mathbf{H}_{xz}(s,t) &= \begin{bmatrix}1&0&0\\s&1&t\\0&0&1\end{bmatrix} \\ \mathbf{H}_{yz}(s,t) &= \begin{bmatrix}1&s&t\\0&1&0\\0&0&1\end{bmatrix} \end{align}

5.6 组合变换

因为几个变换矩阵的大小是相同的，所以多个变换矩阵可以被结合在一起。如在物体坐标系中的物体，需要转换到世界坐标系中，此时需要使用模型变换（Model Transform，表示为Mobj→wld\mathbf{M}_{obj\rightarrow wld}），将物体从世界坐标系中转换到摄像机坐标系，需要使用视图变换（View Transform，表示为Mwld→cam\mathbf{M}_{wld\rightarrow cam}）。它们的数学表述如下：

Pwld=pobjMobj→wldPcam=pwldMwld→cam=(pobjMobj→wld)Mwld→cam\begin{align} \mathbf{P}_{wld}&=\mathbf{p}_{obj}\mathbf{M}_{obj\rightarrow wld} \\ \mathbf{P}_{cam}&=\mathbf{p}_{wld}\mathbf{M}_{wld\rightarrow cam} \\ &= (\mathbf{p}_{obj}\mathbf{M}_{obj\rightarrow wld})\mathbf{M}_{wld\rightarrow cam} \end{align}

矩阵的乘法是满足结合律的，所以可以得到：

Pcam=(pobjMobj→wld)Mwld→cam=pobj(Mobj→wldMwld→cam)\begin{align} \mathbf{P}_{cam} &= (\mathbf{p}_{obj}\mathbf{M}_{obj\rightarrow wld})\mathbf{M}_{wld\rightarrow cam} \\ &= \mathbf{p}_{obj}(\mathbf{M}_{obj\rightarrow wld}\mathbf{M}_{wld\rightarrow cam}) \end{align}

可以连接顶点循环外的矩阵，并且在循环内只有一个矩阵乘法（有很多顶点），具体如下：

Mobj→cam=Mobj→wldMwld→camPcam=PobjMobj→cam\mathbf{M}_{obj\rightarrow cam}=\mathbf{M}_{obj\rightarrow wld}\mathbf{M}_{wld\rightarrow cam} \\ \mathbf{P}_{cam} = \mathbf{P}_{obj}\mathbf{M}_{obj\rightarrow cam}

5.7 变换的分类

当讨论一般的变换时，可以使用同义词映射（Mapping）或函数（Function）。在一般意义上，映射只是一个接受输入并产生输出的规则。如将F\mathbf{F}将a\mathbf{a}映射至b\mathbf{b}，可以表示为F(a)=b\mathbf{F(a)=b}(读作a等于b的F)。

5.7.1 线性变换(Linear Transformations)

如果映射F(a)\mathbf{F}(a)是线性的，那么满足：

F(a+b)=F(a)+F(b)且F(ka)=kF(a)\mathbf{F(a+b)=F(a)+F(b)} \\且\\ \mathbf{F}(k\mathbf{a})=k\mathbf{F(a)}

线性变换的定义还有两个含义。

  1. 映射F(a)=aM\mathbf{F(a)=aM}（其中，M\mathbf{M}是任意方形矩阵）是一个线性变换，因为：

F(a+b)=(a+b)M=aM+bM=F(a)+F(b)且F(ka)=(ka)M=k(aM)=kF(a)\mathbf{F(a+b)=(a+b)M=aM+bM=F(a)+F(b)} \\且\\ \mathbf{F}(k\mathbf{a})=(k\mathbf{a})\mathbf{M}=k(\mathbf{aM})=k\mathbf{F(a)}

可以通过矩阵乘法实现的任何变换都是线性变换。

  1. 任何线性变换，输入是零向量，输出必然也是零向量。如果F(0)=a,a≠0\mathbf{F(0)=a,a\neq0},则F\mathbf{F}不能是线性变换，因为F(k0)=a\mathbf{F}(k\mathbf{0})=a,所以F(k0)≠kF(0)\mathbf{F}(k\mathbf{0})\neq k\mathbf{F(0)}。

线性变换不包含平移。

5.7.2 仿射变换(Affine Transformations)

仿射变换（Affine）是线性变换，然后加上平移。因此，仿射变换集是该组线性变换的超集：任何线性变换都是仿射变换，但并非所有仿射变换都是线性变换。

形如v′=vM+b\mathbf{v^{'}=vM+b}的任何变换都是仿射变换。

5.7.3 可逆变换(Invertible Transformations)

如果一个变换是可逆的，即存在一个相反的变换可以重置之前的变换，表达式如下：

F−1(F(a))=F(F−1(a))=a\mathbf{F^{-1}(F(a))=F(F^{-1}(a))=a}

因为位移操作必然是可逆的，所以仿射变换是否可逆的关键在于线性变换是否可逆。主要的线性变换，除了投影外都是可逆的，因为投影变换将一个维度的数值变为了零，即一个维度的数据消失了。

找出一个变换的相反操作，相当于找出这个变换矩阵的逆矩阵。如果一个矩阵没有逆矩阵，称这个矩阵为奇异矩阵（或退化矩阵，Singular Matrix）。可逆矩阵的行列式是非零的。

在非奇异矩阵中，零向量是唯一的输入向量，它被映射到输出空间中的两向量，所有其他向量都映射到其他的一些非零向量。而在奇异矩阵中，有一系列的输入向量都会导致输出为零向量，这些输入向量称为矩阵的零空间（Null Space），其被映射到零向量。在投影矩阵中，垂直于投影平面的所有向量都在零空间中，因为这些向量在投影后会变成一个点。

对于一个方阵，如果它的基础向量（因为本书用的是行向量，所以相当于每一行，如果用的是列向量则相当于每一列）是线性相关的，则这个矩阵是歧义矩阵，即不存在逆矩阵。

5.7.4 保角变换(Angle-preserving Transformations)

如何两个向量之间的角度再变换后的大小或方向上没有改变，则该变换就是保角变换。只有位移，旋转，和均匀缩放是保角变换。对于反射变换，虽然角度的绝对值不会发生改变，但是角度的方向发生了改变，因此也不能算是保角变换。所有的保角变换都是仿射变换且都是可逆的。

5.7.5 正交变换(Orthogonal Transformations)

正交变换可以很容易的求出反变换，所以被使用的频率很高。正交变换保证变换前后，图像的长度，角度的绝对值，面积和体积不会发生改变。只有位移，旋转和反射是正交变换。所有的正交变换都是可逆的，且是仿射变换。

5.7.6 刚体变换(Rigid body Transformations)

刚体变换是指改变对象的位置和方向但不改变其形状的变换。保留所有角度、长度、面积和体积。平移和旋转都是刚体变换，但是反射不被认为是严格的刚体变换。

刚体变换也称为合适变换（Proper Transformation）。所有刚体变换都是正交变换、保教变换、可逆变换和仿射变换。

任何刚体变换矩阵的行列式均为1。

5.7.7 变换类型总结

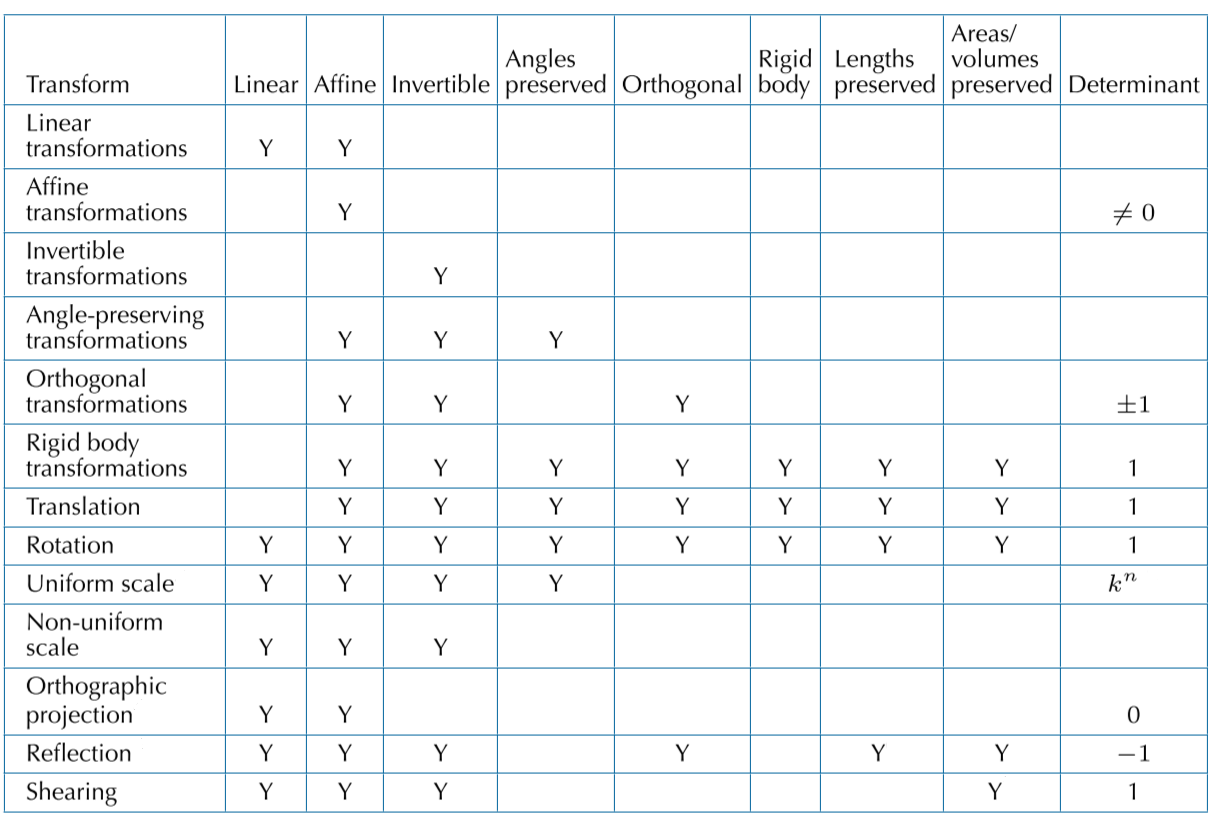
变换的类型

引用：

  1. Dunn, F. and Parberry, I. (2011). 3D math primer for graphics and game development 2nd2^{nd}.