2.1 向量和其它无聊东西的数学定义
对数学家来说,向量就是一个数字列表,对程序员来说向量可以数组(Array)表示,但在计算机的图形开发中我们侧重于向量的几何表示。数学家会区分向量和标量(Scalar)。
-
向量:指具有大小和方向的量。如:速度(Velocity)和位移(Displacement)。
-
标量:只具有数值大小,而没有方向等其他意义,部分有正负之分。如:速率(Speed)和距离(Distance)。
-
向量的维度:向量的维度表示向量中元素的个数。一个元素就是一维向量,两个数元素就是二维向量,三个元素就是三维向量…
-
向量表达:在书写向量时,有两种表达方式:水平写入和垂直写入,水平写入的向量称为行向量(Row Vector),垂直写入的称为列向量(Column Vector)。
三维列向量
xyz
线性代数:研究向量和矩阵的数学称为线性代数(linear algebra)。在线性代数中,n维度的向量和矩阵是用来求解有n个未知数的方程的。而在这本书中解释了向量和与矩阵的几何与几何意义。
2.2 向量的几何定义
矢量:在数学上讨论的向量,在几何学中可称为矢量。它是具有大小(Magnitude)和方向(Direction)的有向线段。在图形上常用箭头(起点指向终点)表示,因为它捕获了向量的两个定义特征:大小和方向。向量并没有位置信息,大小和方向一致的向量出现在图中的什么位置并没有区别。
- 向量的大小:向量的长度。向量是可以具有任何非负长度。
- 向量的方向:向量在空间中指向的方向。方向(Direction)不等于定向(Orientation)。
2.3 使用笛卡尔坐标指定向量
当使用笛卡尔坐标来描述向量时,向量中的每个元素表示对应的坐标的有符号位移。如[2,3]表示X轴方向移动了2,y轴方向移动了3,位移的顺序并没有关系。
零向量:它是唯一的一个大小为零的向量,唯一没有方向的向量,所以它的描绘为点。可以将零向量看作是表达“无位移”概念的一种方式。零向量是作为加法单位元(additive identity,加到别的元素上也不会造成区别的数字)。
2.4 向量与点
点(Points)表示位置,向量(Vectos)表示位移。
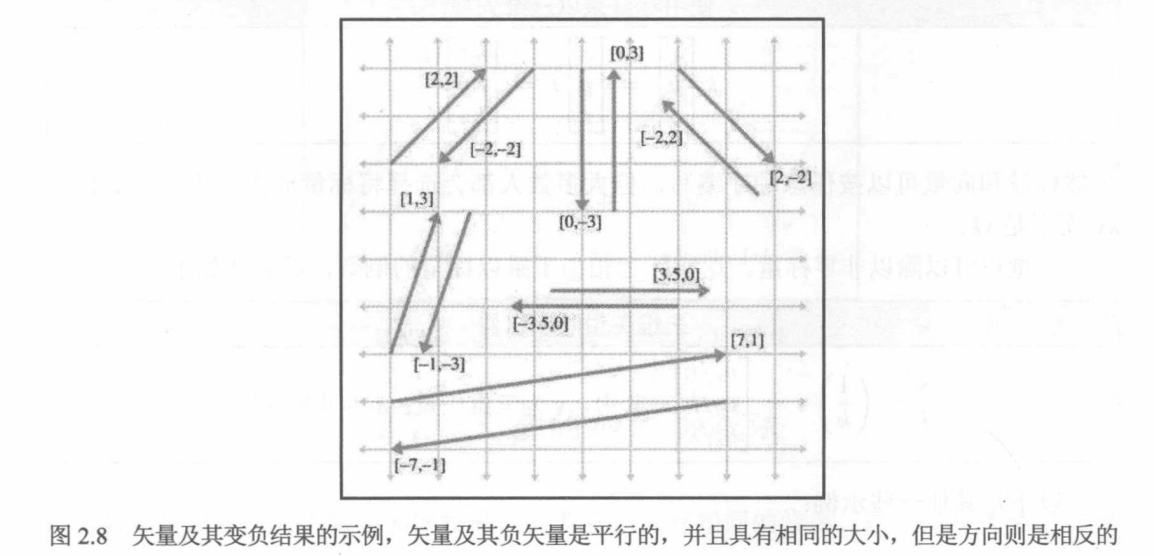
2.5 负向量
2.5.1 正式线性代数规则
让向量变负
−a1a2⋮an−1an=−a1−a2⋮−an−1−an
让二维、三维和思维向量变负
−[xy]=[−x−y],−[xyz]=[−x−y−z],−[xyzw]=[−x−yz−w]
2.5.2 几何解释
向量的位置无关紧要的——只有大小和方向很重要。
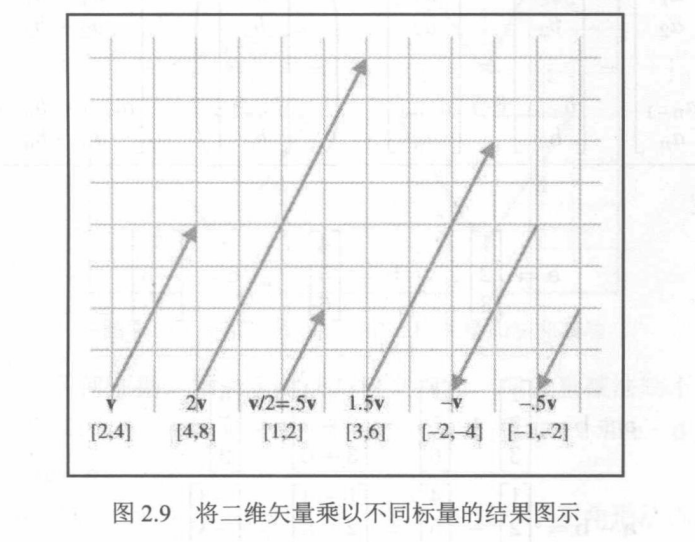
2.6 标量和向量的乘法
向量和标量不能相加,但可以将向量乘以标量。结果是一个与原始向量平行的向量,当具有不同的长度和可能相反的方向。
2.6.1 正式线性代数规则
使用标量乘以向量
ka1a2⋮an−1an=a1a2⋮an−1ank=ka1ka2⋮kan−1kan
使用标量乘以三维向量
kxyz=xyzk=kxkykz
三维向量除以非零标量
kv=(k1)=vx/kvy/kvz/k
- 当将向量乘以标量时,不必使用任何乘法符号。乘法是通过将两个量并排放置(通常右边的是向量)来表示。
- 标量和向量的乘法和除法都在任何加法和减法之前发生。
- 标量无法乘以向量,向量也无法除以另一个向量。
- 负向量可以被视为将向量乘以-1的特殊情况。
2.6.2 几何解释
在几何上,将向量乘以标量k具有将长度缩放|k|因子的效果。
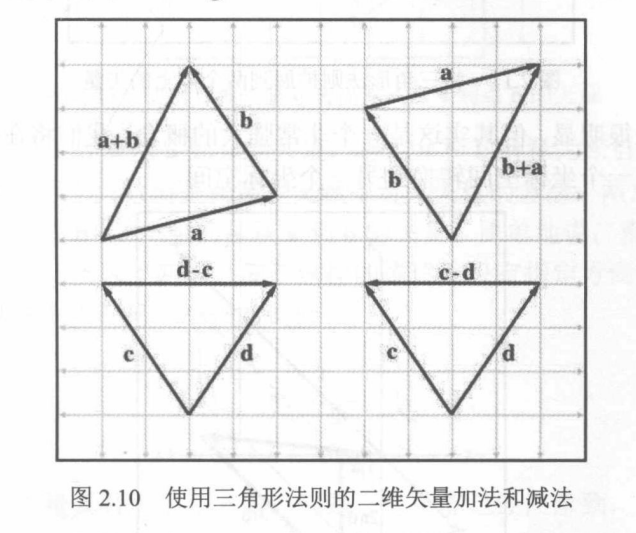
2.7 向量的加法和减法
我们可以让两个向量相加或相减,只要它们具有相同的维度。结果是与向量运算项具有相同维度的向量。向量加法和减法的表示法与标量的加法和减法的表示法是一样的。
2.7.1 正式线性代数规则
向量的加法
a1a2⋮an−1an+b1b2⋮bn−1bn=a1+b1a2+b2⋮an−1+bn−1an+bn
向量的减法
a1a2⋮an−1an−b1b2⋮bn−1bn=a1a2⋮an−1an+−b1b2⋮bn−1bn=a1−b1a2−b2⋮an−1−bn−1an−bn
加法满足交换率
a + b = b + a
减法不满足交换律
a - b = - (b - a)
2.7.2 几何解释
三角形法则:如果从一个点开始应用a指定的位移,然后再应用由b指定的位移,那就像应用了单个位移a+b一样。这称为向量加法的三角形法则(Triangle Rule)。它也适用于向量减法。
向量加法是可以交换的,但是向量减法则不是。
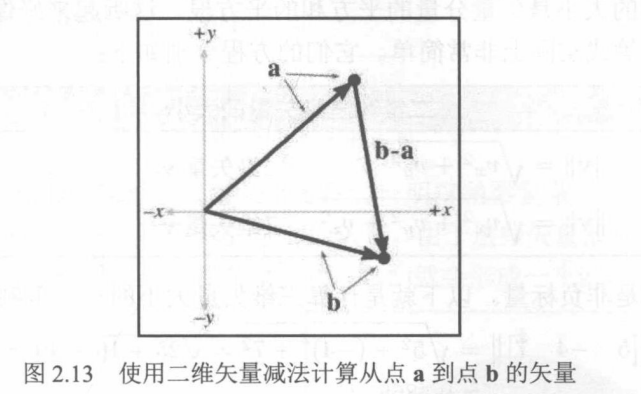
2.7.3 从一点到另一点的位移向量
当要计算从点a到点b的位移向量,可以通过b−a获得.
2.8 向量大小
向量的大小也称为向量的长度(Length)或模(Norm)。它的值是非负的。
正式线性代数规则
任意维度的矢量大小
矢量的大小是矢量分量的平方和的平方根。
∣∣v∣∣=i=1∑nvi2=v12+v22+⋯+vn−12+vn2
二维和三维矢量的大小
∣∣v∣∣=vx2+vy2二维矢量v∣∣v∣∣=vx2+vy2+vz2三维矢量v
几何解释
毕达哥拉斯定理指出,对于任何直角三角形,斜边长度的平方等于另外两边长度的平方和。则有
∣∣v∣∣2=∣vx∣2+∣vy∣2∵∣x∣2=x2∴∣∣v∣∣=vx2+vy2∴∣∣v∣∣2=vx2+vy2∴∣∣v∣∣=vx2+vy2
对于任何正大小m,存在无数个大小为m的矢量。由于这些矢量都具有相同的长度只是方向不同,因此,将它们的尾部放置在原点时,他们就会形成一个圆。
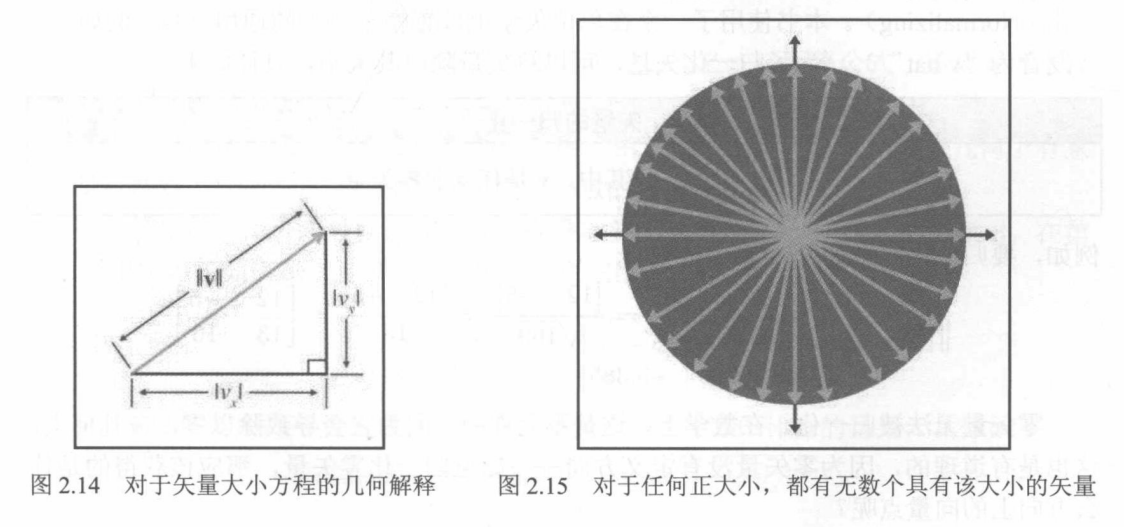
2.9 单位向量
对于许多向量,我们只关注其方向而不是大小,在这些情况下,使用单位向量通常会更方便。例如:法线(Normal)。
单位向量(Unit Vector)是大小为1的向量。单位向量也被称为归一化向量(Normalized Vector)。
2.9.1 正式线性代数规则
对于任何非零向量v,可以计算指向与v相同方向的单位向量,此过程称为向量的归一化(Normalizing)。零向量无法被归一化,在数学上是因为除零规则,在几何上是因为零向量没有定义方向。
向量的归一化
v^=∣∣v∣∣v其中,v是任意非零向量
∣∣[12−5]∣∣[12−5]=122+52[12−5]=169[12−5]=13[12−5]=[131213−5]
2.9.2 几何解释
在二维中,如果将单位向量的尾部绘制在原点处,则矢量的头部将接触到以原点为中心的单位圆(单位圆的半径为1)。在三维中,单位向量接触到的是单位球面。
请注意,向量长度大于1时,对向量进行归一化会使它更短;向量长度小于1时,对向量进行归一化会使它更长。
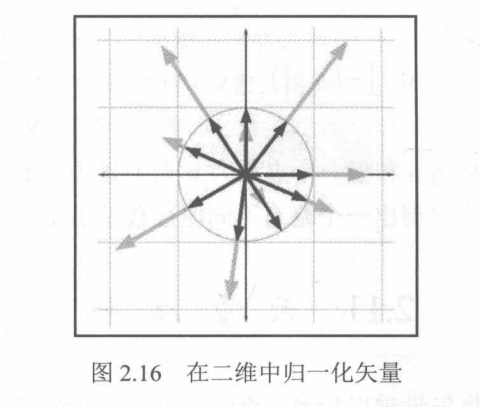
2.10 距离公式
距离为两点之间的线段长度。由于向量是有向线段,因此几何上有意义的是,两点之间的距离将等于从一点到另一点的向量的长度。
d=b−a=bx−axby−aybz−az
- a和b之间的距离等于向量d的长度(注意,此处,谁看作a,谁看作b无关紧要):
distance(a,b)=∣∣d∣∣=dx2+dy2+dz2
三维距离公式
distance(a,b)=∣∣d∣∣=(bx−ax)2+(by−ay)2+(bz−az)2
二维距离公式
distance(a,b)=∣∣d∣∣=(bx−ax)2+(by−ay)2
2.11 向量点积
向量点积(dot product)又称为向量内积(inner product)。点积的结果是标量。
2.11.1 正式线性代数规则
向量点乘时必须用一个使用点符号,如 a⋅b。如果看到两个向量并排放置,中间没有符号,则需要根据矩阵乘法的规则进行解释。
矢量点积
a1a2⋮an−1an⋅b1b2⋮bn−1bn=a1b1+a2b2+⋯+an−1bn−1+anbn
使用求和符号表示的向量点积
a⋅b=i−1∑naibi
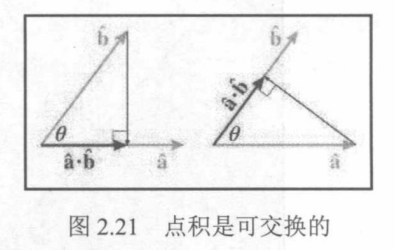
向量点积是可交换的:a⋅b=b⋅a。
2.11.2 几何解释
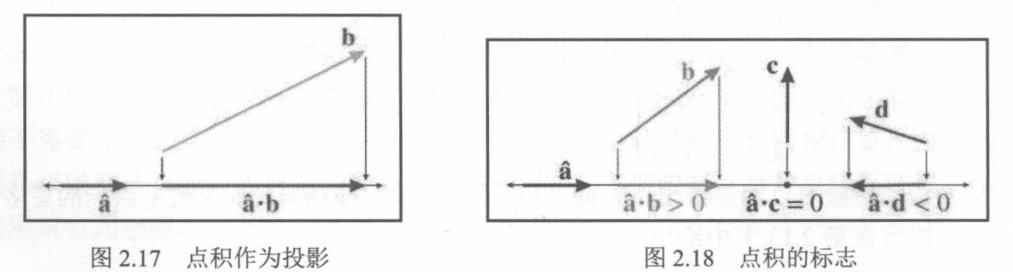
投影
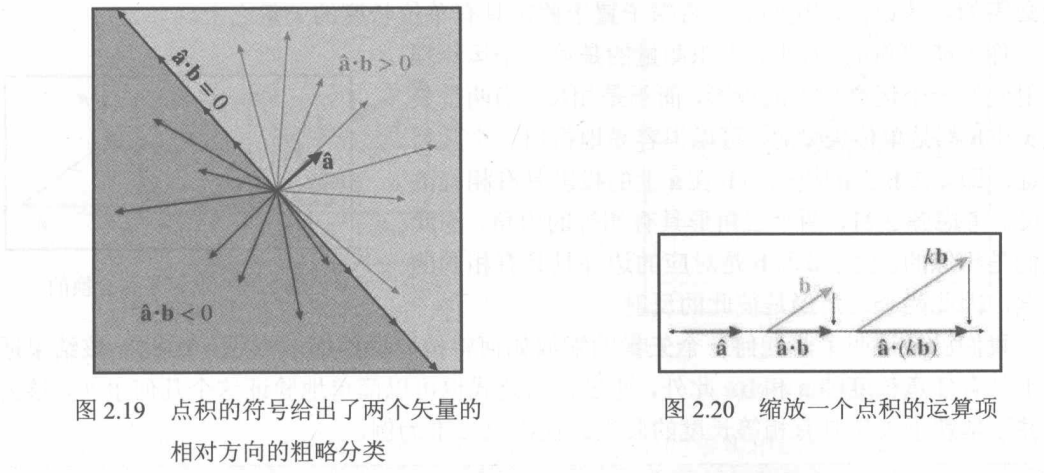
点积a⋅b等于b投影到平行于a的任何线上的有符号长度,乘以a的长度。点积的符号可以给予我们对两个向量的相对方向的粗略分类。当b产生缩放时,它在a^上的投影长度随着点积值的增加而增加。
点积与任意向量和标量的乘法的结合律
(ka)⋅b=k(a⋅b)=a⋅(kb)
当两个向量a^和b^都是单位向量时,可以很容易得出一个论证,即a^和b^上的投影与b^在a^上的投影具有相同的长度。点积结果时标量,因此也能推断出点积是可以交换的。
点积是可交换的
a⋅b=axbx+ayby=bxax+byay=b⋅a
点积分布
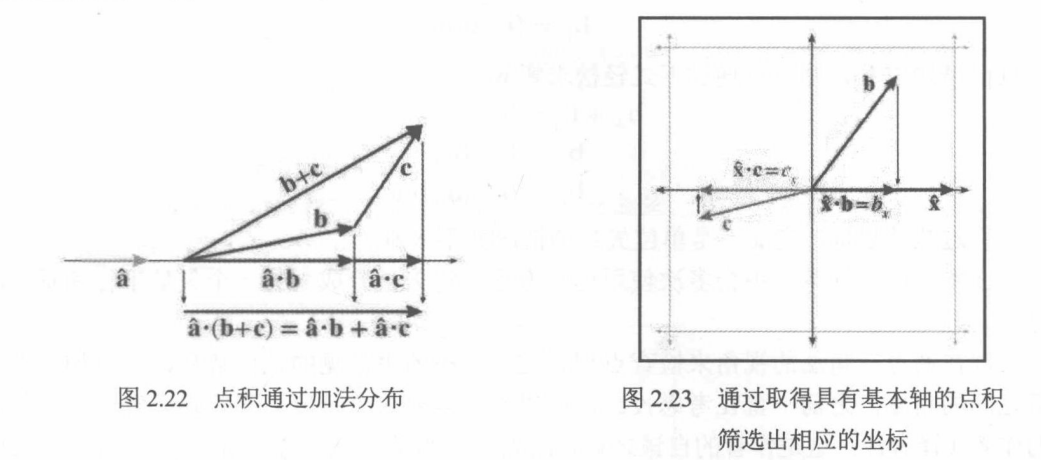
就像标量乘法一样,通过加法和减法进行分布。如果点积的运算项之一是一个总和值,那么就可以单独取得各个部分的点积,然后取它们的总和。
点积通过加法和减法进行分布
a⋅(b+c)=axayax⋅bx+cxby+cybz+cz=ax(bx+cx)+ay(by+cy)+az(bz+cz)=axbx+axcx+ayby+aycy+azbz+azcz=(axbx+ayby+azbz)+(axcx+aycy+azcz)=a⋅b+a⋅c
通过用−c替换c,可以得知,点积也可以通过向量减法进行分布,就像向量加法一样。还可以通过取得具有基本轴的向量的点积“筛选”出该轴的坐标。
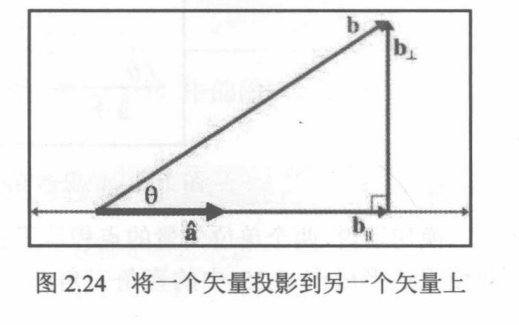
b在a上的投影实际上可以看作是b在a方向上的分量。因此还可以通过投影来将b拆分为两部分:b∣∣和b⊥(”b平行“和“b垂直”),平行于a的分量和垂直与a的分量。已知b∣∣的长度等于a^⋅b,但是b∣∣是一个分量,所以将采用单位矢量a^指定的方向并将其放大,表述如下:
b∣∣=(a^⋅b)a^
已知b∣∣,则可推导b⊥:
b⊥+b∣∣b⊥b⊥=b=b−b∣∣=b−(a^⋅b)a^
点积截取角度
通过直接三角形来解释点积:
cosθ=斜边(hypotenuse)邻边(adjacent)=1a^⋅b^=a^⋅b^
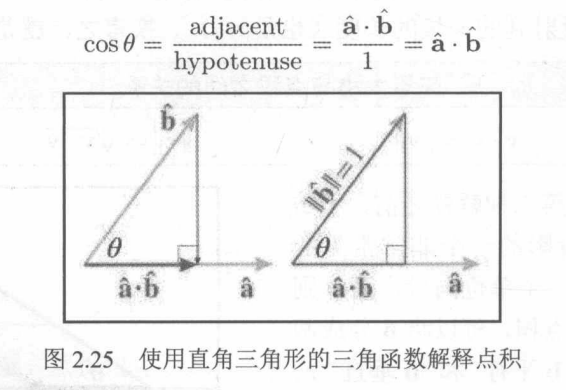
两个向量a和b的点积等于向量之间角度θ的余弦,乘以向量的长度。
a⋅bθθ=∣∣a∣∣ ∣∣b∣∣cosθ=arccos(∣∣a∣∣ ∣∣b∣∣a⋅b)=arccos(a^⋅b^)(假设a^和b^都是单位向量)
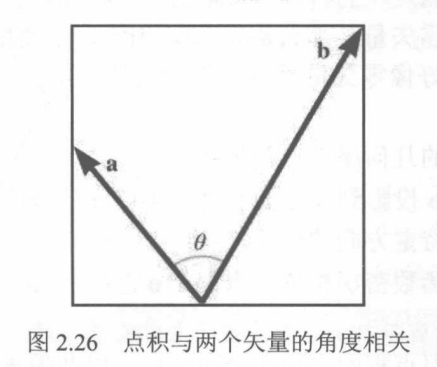
点积的符号可以用作两个向量之间角度的粗略分类
| a^⋅b^ |
θ |
角度为 |
a和b是 |
| > 0 |
0∘≤θ<90∘ |
锐角 |
主要指向同一方向 |
| 0 |
θ=90∘ |
直角 |
垂直 |
| < 0 |
90∘<θ<180∘ |
钝角 |
主要指向相反方向 |
公式推导
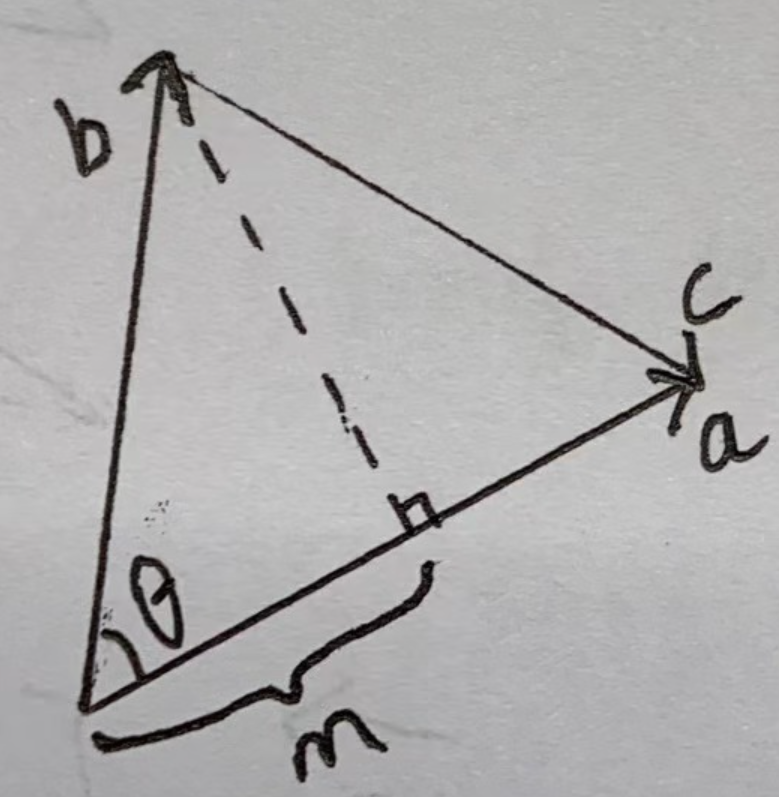
转载来源:https://www.cnblogs.com/sf5803/p/14354300.html
如图所示:b与b的夹角为θ,c=a−b,a,b,c构成一个三角形。
由三角形余弦定理可知:
∣∣c∣∣=∣∣b∣∣2+∣∣c∣∣2−2∣∣a∣∣ ∣∣b∣∣cosθ
假设a=[a1a2],b=[b1b2]:
则由向量大小可知:∣∣a∣∣2=a12+a22,∣∣b∣∣2=b12+b22
余弦定理推导如下:
则有:
∣∣c∣∣2=∣∣(a−b)∣∣2=∣∣[a1−b1a2−b2]∣∣2=(a1−b2)2+(a2−b2)2=a12+b12−2a1b1+a22+b22−2a2b2(完全平方差公式)
所以:
a12+b12−2a1b1+a22+b22−2a2b2=a12+a22+b12+b22−2∣∣a∣∣ ∣∣b∣∣cosθ∣∣c∣∣2=∣∣a∣∣2+∣∣b∣∣2−2∣∣a∣∣ ∣∣b∣∣cosθ(余弦定理)
点积几何解释推导如下:
假设a的方向为X轴。
a12+b12−2a1b1+a22+b22−2a2b2a1b1+a2b2a⋅b=a12+a22+b12+b22−2∣∣a∣∣ ∣∣b∣∣cosθ=∣∣a∣∣ ∣∣b∣∣cosθ=a1b1+a2b2=∣∣a∣∣ ∣∣b∣∣cosθ
可证:
a⋅b则:∣∣b∣∣cosθ=∣∣a∣∣a⋅b=a1a2⋮an−1an⋅b1b2⋮bn−1bn=a1b1+a2b2+⋯+an−1bn−1+anbn=∣∣a∣∣ ∣∣b∣∣cosθ
投影公式的推导如下:
假设m为投影向量。
cosθ=斜边邻边=∣∣b∣∣∣∣m∣∣∴∣∣m∣∣=∣∣b∣∣cosθ=∣∣a∣∣a⋅b∵a^=∣∣a∣∣a∴∣∣m∣∣=a^⋅b∴b∣∣=a^⋅b
另一种点积几何公式推导法:
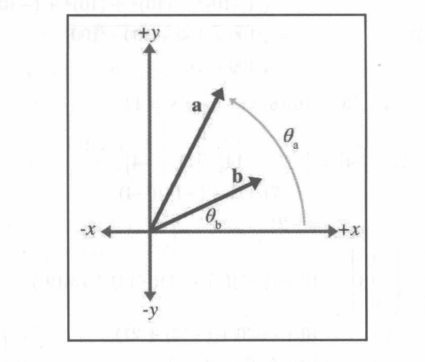
由图可知:
axaybxby=∣∣a∣∣cosθa,=∣∣a∣∣sinθa,=∣∣b∣∣cosθb,=∣∣b∣∣sinθb
则有点积的代数定义:
a⋅b=axbx+ayby=∣∣a∣∣cosθa∣∣b∣∣cosθb+∣∣a∣∣sinθa∣∣b∣∣sinθb=∣∣a∣∣ ∣∣b∣∣(cosθacosθb+sinθasinθb)=∣∣a∣∣ ∣∣b∣∣cos(θb−θa)=∣∣a∣∣ ∣∣b∣∣cosθ
总结
- 点积a⋅b将测量b投影到a上的长度,乘以a的长度。
- 点积可用于测量特定方向的位移。
- 投影运算与余弦函数密切相关。点积a⋅b也等于∣∣a∣∣ ∣∣b∣∣cosθ,其中,θ是向量之间的角度。
2.12 向量叉积
叉积(Cross Product)又叫外积或向量积(Vector Product),只能在三维中应用。叉积将产生一个新的向量。
2.12.1 正式线性代数规则
叉乘公式
x1y1z1×x2y2z2=y1z2−z1y2z1x2−x1z2x1y2−y1x2
-
叉积和点积具有相同的运算符优先级:乘法发生在加法和减法之前。运算a⋅b×c=a⋅(b×c)被称为三重积。
-
向量的叉积不满足交换律:a×b=b×a
-
向量的叉积满足反转换:a×b=−(b×a)
-
向量的叉积不满足结合律:(a×b)×c=a×(b×c)
-
标量与叉积满足结合律:k(a×b=(ka)×b=a×(kb)
2.12.2 几何解释
叉积将产生一个新的向量,垂直于原始的两个向量。其大小等于两个向量的大小乘上两个向量之间夹角的sin,该大小也等于由两个向量构成的平行四边形的面积。
叉积的大小与向量之间的角度的正弦值有关
∣∣a×b∣∣=∣∣a∣∣ ∣∣b∣∣sinθ
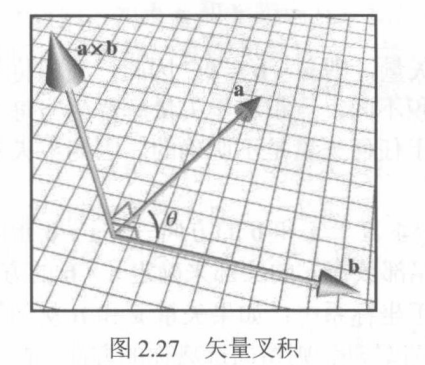
我们可以通过将b的尾部放在a的头部来确定a×b的方向,并检查是否从a到b顺时针或逆时针转动。在左手坐标系下,如果在形成的方向是顺时针的,则结果方向指向外侧,如果是逆时针,则指向内侧。在右手坐标系下,结果相反。
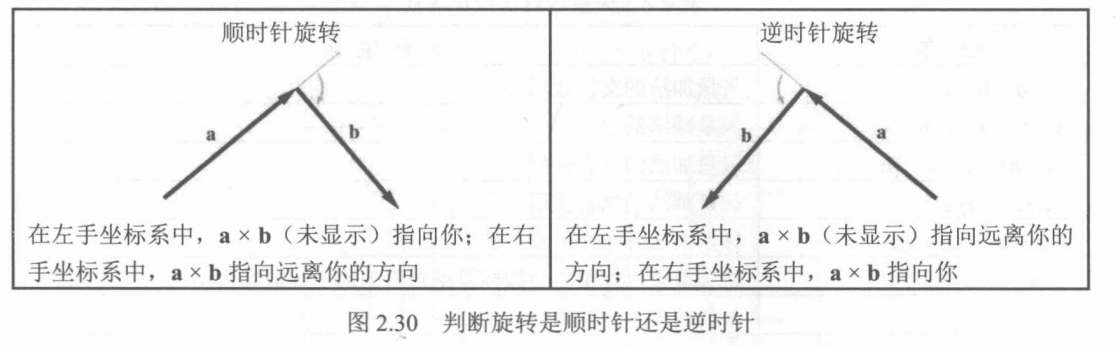
公式推导
假设a和b的叉积为:m,则有
abm=x1y1z1,=x2y2z2,=y1z2−z1y2z1x2−x1z2x1y2−y1x2
那么计算向量m的长度平方,则有:
∣∣m∣∣2=(y1z2−z1y2)2+(z1x2−x1z2)2+(x1y2−y1x2)2=(y1z2)2+(z1y2)2−2y1y2z1z2+(z1x2)2+(x1z2)2−2x1x2z1z2−(x1y2)2+(y1x2)2−2x1x2y1y2=(x12+y12+z12)×(x22+y22+z22)−(x1x2+y1y2+z1z2)2=∣∣a∣∣2∣∣b∣∣2−(a⋅b)2=∣∣a∣∣2∣∣b∣∣2−(∣∣a∣∣2∣∣b∣∣2cosθ)2=∣∣a∣∣2∣∣b∣∣2(1−cosθ2)=∣∣a∣∣2∣∣b∣∣2sinθ2=(∣∣a∣∣ ∣∣b∣∣sinθ)2
可证:∣∣a×b∣∣=∣∣m∣∣=∣∣a∣∣ ∣∣b∣∣sinθ
2.13 线性代数恒等式
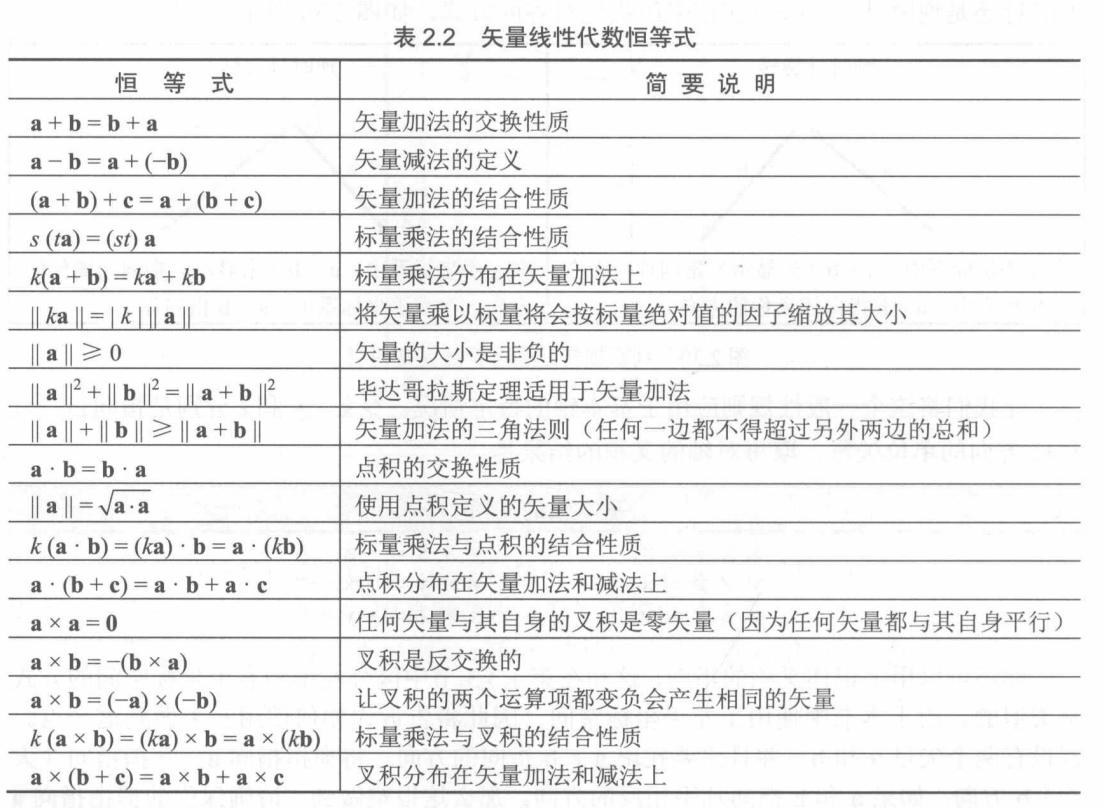
引用:
- Dunn, F. and Parberry, I. (2011). 3D math primer for graphics and game development 2nd.



















