所谓“3D数学”就是以数学方式精确地测量在三维空间中的位置、距离和角度。使用计算机执行此类计算的最常用的框架称为笛卡尔坐标系(Cartesian coordinate system)。
1.1 一维数学
自然数(Natural Number)是指用以计量事物的件数或表示事物次序的数。
有理数(Rational numbers)定义:可以表示为两个整数的比 实数定义:包括有理数和无理数(例如π)
对于自然数和整数的研究称作为离散数学(Discrete Mathematics),对于实数的学习称为连续数学(Continuous Mathematics)。
计算机图形学第一定律:如果它看起来正确,那就是对的。
1.2 二维笛卡尔空间
二维笛卡尔坐标空间就是我们常说的直角坐标系,二维笛卡尔坐标空间是可以无限延伸的。二维笛卡尔坐标空间由以下两条信息定义:
- 每个二维笛卡尔坐标空间都有一个特殊的位置,称为原点(Origin),它是坐标的中心。
- 每个二维笛卡尔坐标空间都有两条直线通过原点,每条线都称为轴(Axis),并且可以在两个相反的方向上无限延伸。
对于二维坐标而言,无论X轴和Y轴选取的方向如何,总是可以旋转坐标空间。坐标空间是用于精确指定位置的框架。
1.3 三维笛卡尔空间
所有的三维坐标空间都不相等,因为某些坐标系对不能相互对齐。有以下两种不同类型的三维坐标空间:左手坐标空间和右手坐标空间。如果两个坐标空间具有相同的旋向性(Handedness),则可以旋转它们使得轴对齐:如果两个坐标空间的旋向性相反,那么这就是不可能的。

左手坐标系与右手坐标系的转换:交换一个轴的正负端即可。
首先左手握拳,然后竖起大拇指,大拇指指向旋转轴的正方向(正值端);此时,围绕旋转轴的正向旋转方向就是其它四个手指卷曲的方向。在左手坐标系中,从旋转轴的正向看正向旋转的方向是顺时针的。
首先右手握拳,然后竖起大拇指,大拇指指向旋转轴的正方向(正值端);此时,围绕旋转轴的正向旋转方向就是其它四个手指卷曲的方向。在右手坐标系中,从旋转轴的正向看正向旋转的方向是逆时针的。
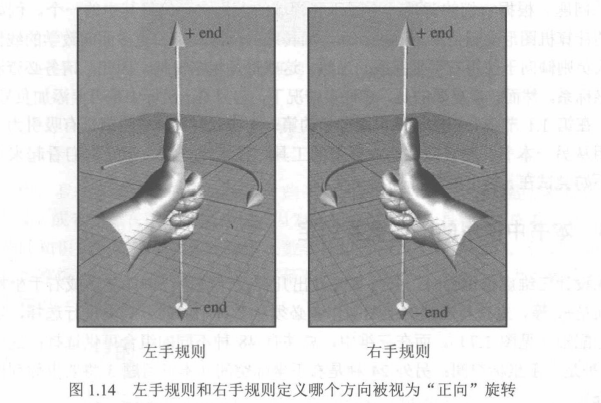
本书使用左手坐标系。
1.4 一些零散的基础知识介绍
i=1∑nai=a1+a2+a3+...+an
i=1∏nai=a1×a2×a3×...×an
闭区间(Closed Interval)也称为包含(Inclusive)区间,用” [ ”和” ] ”表示。
开区间(Open Interval)也称为排除(Exclusive)区间,用” ( ”和” ) ”表示。
[a,b]表示a≤x≤b(a,b)表示a<x<b[a,b)表示a≤x<b(a,b]表示a<x≤b
角度可以用度数(Degree)和弧度(Radian)表示。
弧度:1rad=(180/π)∘≈57.29578∘度数:1∘=(π/180)rad≈0.01745329rad
在一个直角三角形中,斜边为:𝑟,其中一条直角边为:𝑥,另一条直角边为:𝑦,直角边𝑥与斜边𝑟的夹角为:𝜃,则:
正弦:sinθ=y/r(对边/斜边)余弦:cosθ=x/r(邻边/斜边)正切:tanθ=y/x(对边/邻边)正割:secθ=r/x(斜边/邻边)余割:cscθ=r/y(斜边/对边)余切:cotθ=x/y(邻边/对边)推导出:secθ=cosθ1tanθ=cosθsinθcosθ=sinθ1cotθ=tanθ1=sinθcosθ
与对称性相关的基本恒等式
sin(−θ)=−sinθ,cos(−θ)=cosθ,tan(−θ)=−tanθ.sin(2π−θ)=cosθ,cos(2π−θ)=sinθ,tan(2π−θ)=cotθ
毕达哥拉斯定理
a2+b2=c2
毕达哥拉斯恒等式
sin2θ+cos2θ=1.1+tan2θ=sec2θ.1+cot2θ=csc2θ
和或差恒等式
sin(a+b)=sinacosb+cosasinb,sin(a−b)=sinacosb−cosacosb,cos(a+b)=cosacosb−sinasinb,cos(a−b)=cosacosb+sinasinb,tan(a+b)=1−tanatanbtana+tanb,tan(a−b)=1+tanatanbtana−tanb
等腰三角形恒等式
sin2θ=2sinθcosθ,cos2θ=cos2θ−sin2θ=2cos2θ−1=1−2sin2θ,tan2θ=1−tan2θ2tanθ
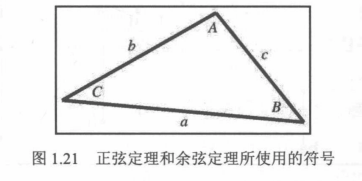
正弦定理
asinA=bsinB=csinC
余弦定理
a2=b2+c2−2bccosA,b2=a2+c2−2accosB,c2=a2+b2−2abcosC
引用:
- Dunn, F. and Parberry, I. (2011). 3D math primer for graphics and game development 2nd.




