3D数学基础：图形和游戏开发 读书笔记 第8章

¶8.1 "定向"含义探微

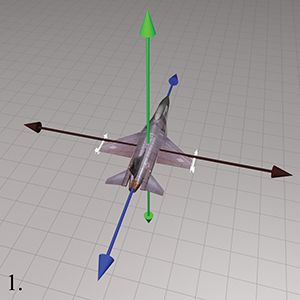
方向（DIrection）可以用两个数字（也就是球面坐标的角度）设置三维中的方向的参数；而定向（Orientation）则至少需要三个数字（欧拉角）。如下图飞机的方向需要两个参数，而定向还需要绿圈方向来决定其旋转角度（旋转量称为角位移（Angular Displacement）。

¶8.2 矩阵形式

描述三维中坐标空间的定向的一种方法是告诉该坐标空间（$+x$轴，$+y$轴和$+z$轴）的基向量指向那个方向。我们可以用这些向量形成$3 \times 3$矩阵的行时，就是用矩阵形式表示了定向。

¶8.2.1 矩阵的选择

矩阵可以将点从一个坐标空间变换为另一个坐标空间，其中两个用的比较多的方法时：

• 获取对象空间向量并以直立坐标表示。
• 获取直立空间向量并以对象坐标表示。

特殊的$3 \times 3$矩阵类很有用，它专门用于存储对象的定向，而不是任意变换。该类假设矩阵是正交的，这意味着他作为一个不变量，只包含旋转（也能假设矩阵不包含反射，即使在正交矩阵中也是如此）。

¶8.2.2 方向余弦矩阵

“方向余弦(Direction Cosine)矩阵”是由两组不同的标准正交基的基向量之间的方向余弦所形成的矩阵。方向余弦矩阵可以用来表达一组标准正交基与另一组标准正交基之间的关系，也可以用来表达一个向量对于另一组标准正交基的方向余弦。

假设坐标空间的基向量是相互正交的单位向量$\mathbf{p、q和r}$，而具有相同原点的第二个坐标空间的基向量是不同的（但也正交）基向量$\mathbf{p^{'}、q^{'}和r^{'}}$。将行向量从第一个空间旋转到第二个空间的旋转矩阵可以用每对基向量之间的角度的余弦构造。两个单位矩阵的点积正好等于他们之间的余弦，所以矩阵乘积是：

$$\mathbf{v}\begin{bmatrix} \mathbf{p \cdot p^{'}} & \mathbf{q \cdot p^{'}} & \mathbf{r \cdot p^{'}} \\ \mathbf{p \cdot q^{'}} & \mathbf{q \cdot p^{'}} & \mathbf{r \cdot q^{'}} \\ \mathbf{p \cdot r^{'}} & \mathbf{q \cdot r^{'}} & \mathbf{r \cdot r^{'}} \end{bmatrix}=\mathbf{v^{'}}$$

这些轴可以被解释为几何而不是数字实体，因此，用什么坐标来描述轴都无关紧要（假设使用相同的坐标空间来描述它们），旋转矩阵将是一样的。

• 旋转矩阵的行是输出坐标空间的基向量，通过使用输入坐标空间的坐标表示。

$$\begin{bmatrix} \begin{bmatrix}1&0&0\end{bmatrix} \cdot \mathbf{p^{'}} & \begin{bmatrix}0&1&0\end{bmatrix} \cdot \mathbf{p^{'}} & \begin{bmatrix}0&0&1\end{bmatrix} \cdot \mathbf{p^{'}} \\ \begin{bmatrix}1&0&0\end{bmatrix} \cdot \mathbf{q^{'}} & \begin{bmatrix}0&1&0\end{bmatrix} \cdot \mathbf{q^{'}} & \begin{bmatrix}0&0&1\end{bmatrix} \cdot \mathbf{q^{'}} \\ \begin{bmatrix}1&0&0\end{bmatrix} \cdot \mathbf{r^{'}} & \begin{bmatrix}0&1&0\end{bmatrix} \cdot \mathbf{r^{'}} & \begin{bmatrix}0&0&1\end{bmatrix} \cdot \mathbf{r^{'}} \\ \end{bmatrix} = \begin{bmatrix} \mathbf{p_x^{'}} & \mathbf{p_y^{'}} & \mathbf{p_z^{'}} \\ \mathbf{q_x^{'}} & \mathbf{q_y^{'}} & \mathbf{q_z^{'}} \\ \mathbf{r_x^{'}} & \mathbf{r_y^{'}} & \mathbf{r_z^{'}} \end{bmatrix} = \begin{bmatrix} \mathbf{p^{'}} \\ \mathbf{q^{'}} \\ \mathbf{r^{'}} \end{bmatrix}$$

• 旋转矩阵的列由输入空间的基向量形成，使用输出空间的坐标表示。一般而言，转换矩阵不是这样的，它仅使用于正交矩阵，如旋转矩阵。

$$\begin{bmatrix} \mathbf{p} \cdot \begin{bmatrix}1&0&0\end{bmatrix} & \mathbf{q} \cdot \begin{bmatrix}1&0&0\end{bmatrix} & \mathbf{r} \cdot \begin{bmatrix}1&0&0\end{bmatrix} \\ \mathbf{p} \cdot \begin{bmatrix}0&1&0\end{bmatrix} & \mathbf{q} \cdot \begin{bmatrix}0&1&0\end{bmatrix} & \mathbf{r} \cdot \begin{bmatrix}0&1&0\end{bmatrix} \\ \mathbf{p} \cdot \begin{bmatrix}0&0&1\end{bmatrix} & \mathbf{q} \cdot \begin{bmatrix}0&0&1\end{bmatrix} & \mathbf{r} \cdot \begin{bmatrix}0&0&1\end{bmatrix} \\ \end{bmatrix} = \begin{bmatrix} \mathbf{p_x} & \mathbf{q_x} & \mathbf{r_x} \\ \mathbf{p_y} & \mathbf{q_y} & \mathbf{r_y} \\ \mathbf{p_z} & \mathbf{q_z} & \mathbf{r_z} \end{bmatrix} = \begin{bmatrix} \mathbf{p^{T}} & \mathbf{q^{T}} & \mathbf{r^{T}} \end{bmatrix}$$

¶8.2.3 矩阵形式的优点

矩阵形式是表示方向的一种非常明确的形式。这种明确的性质提供了一些好处。

1. 向量的旋转可以立即得到。矩阵形式最重要的属性是，您可以使用矩阵来在对象和竖直空间之间旋转向量。没有其他表示方向的方法可以做到这一点，要旋转向量，我们必须将方向转换为矩阵形式。
2. 图形API使用的格式。部分由于上述原因，图形API使用矩阵来表达方向。（API代表应用程序编程接口。基本上，这是我们用来与图形硬件通信的代码。）当我们与API通信时，我们将不得不将我们的变换表达为矩阵。我们如何在程序内部存储变换取决于我们自己，但如果我们选择另一种表示方法，我们将不得不在图形管道的某个时候将它们转换为矩阵。
3. 多个角位移的连接，允许连续变换。矩阵的第三个优点是，它可以“折叠”嵌套的坐标空间关系。例如，如果我们知道物体A相对于物体B的方向，并且我们知道物体B相对于物体C的方向，那么通过使用矩阵，我们可以确定物体A相对于物体C的方向。我们在第3章讨论嵌套坐标空间时遇到了这些概念，然后在第5.6节中讨论了如何连接矩阵。
4. 矩阵求逆。当一个角位移被表示为矩阵形式时，可以使用矩阵求逆来计算“反向”的角位移。更重要的是，由于旋转矩阵是正交的，所以这个计算只需要转置矩阵即可。

¶8.2.4 矩阵形式的缺点

1. 矩阵存储花费更多的内存。用来表示三维空间旋转的矩阵为$3\times 3$的矩阵，要9个数字，而通过欧拉角只要三个数字。
2. 人类难以使用。矩阵对于人类的直接使用方式而言并不直观。有太多的数字都会被归一到$-1\sim 1$的范围内（为了表示长度位为一的单位向量），还有人类自然会想到角度方向，当矩阵则用向量表示。
3. 矩阵可能存在格式错误。
   1. 并不是随手写一个矩阵都能表示旋转的，旋转矩阵必须是正交矩阵，同时还不能是反转变换。所以矩阵中的数据必须要额外小心，必须满足旋转的表达格式。任何非正交矩阵都不是明确定义的旋转矩阵。反射矩阵（正交）也不是有效的旋转矩阵。
   2. 可能从外部来源获取了错误的数据。例如：运动捕捉数据错误，建模软件不良格式等等。
   3. 可能由精度（浮点输入）不够造成数据错误。因为旋转矩阵中的元素数值通常范围为$-1\sim 1$，当表示一些变换时，精度可能会不够。因此在变换过程中，当小数点后数据进行了舍弃，可能导致无法满足旋转矩阵的性质，这种现象称为矩阵蠕变（Matrix creep）。可以通过矩阵的正交化解决（在第六章有提到）。

¶8.2.5 矩阵形式小结

1. 矩阵是一种表示定向的”强力“方法：可以明确地列出在一些不同空间的坐标中的一个空间的基向量。
2. 术语方向余弦矩阵（Direction Cosine Matrix）暗示旋转矩阵中每个元素等于一个输入基向量于一个输出基向量的点积。与所有变换矩阵一样，矩阵的行是输入空间基向量的输出空间。此外，旋转矩阵的列是输出空间基向量的输入空间，这一事实只有在旋转矩阵中具有正交性的基础上才是真实的。
3. 表示定向的矩阵形式是很有用的，这主要是因为它允许我们在坐标空间之间旋转向量。
4. 现在图形API可通过使用矩阵表示方向。
5. 开发人员可以使用矩阵乘法将嵌套坐标空间的矩阵折叠成单个矩阵。
6. 矩阵求逆提供了一种确定”反向“角位移的机制。
7. 矩阵的内存消耗可能是其他技术的$2 \sim 3$倍。当需要存储大量定向（例如动画数据）时，这可能变成很明显的缺点。
8. 矩阵中的数字对于人类来说并不直观。
9. 并非所有矩阵都可能有效地用于描述定向。对于包含镜像或倾斜的矩阵来说，它们就可能出错。我们也可能会从外部源获取不良数据，或者因为矩阵蠕变而得到格式错误的矩阵。

¶8.3 欧拉角

另一种表示定向的常用方法称为欧拉角（Euler Angles）。

¶8.3.1 欧拉角约定

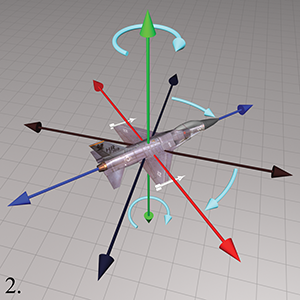
欧拉角将定向描述为围绕3个垂直轴（可以是任意的）的3个旋转。欧拉角主要由”航向-俯仰-滚转“约定，定向由航向角（Heading Angle）、俯仰角（Pitch Angle）和滚转角（Bank Angle）定义。

围绕三个轴的旋转(点击图片可了解绕何轴旋转)如下：

¶8.3.2 其他欧拉角约定

还存在很多其他的欧拉角旋转表达方式，如很常见的yaw-pitch-roll。这种表达方式下，通常roll与bank的含义一模一样，但heading和yaw有细微差别，heading是直立坐标系的y轴，yaw是物体坐标系的y轴。

如果所有的旋转轴都是直立坐标系的轴，则称为固定轴（Fixed-Axis）旋转。而传统的欧拉角旋转都是绕着物体自己的坐标系的轴。两种方式实际上是等效的，只要用相反的顺序执行旋转即可（传统欧拉：yaw-pitch-roll,固定轴：roll-pitch-yaw）。因为传统欧拉角旋转顺序中，前一个轴的旋转会影响后面的轴的位置，而固定轴欧拉角的旋转顺序则不会。

在最原始的欧拉角定义，实际上第一个轴和第三个轴是相同的，这种定义又被命名为proper Euler angles。而现在常用的欧拉角，实际上称为Tait-Bryan angles。

• 这一节中提到个各种命名，并不是绝对的，即可能现在命名名字相同但是含义却不同的情况。
• 在这里提及各种命名，实际上是为了让读者在接触其他的系统时，首先确认下其中的欧拉角定义方式是否不同，如旋转正方向，绕什么轴旋转，绕不同轴旋转的顺序等。
• 不同定义的欧拉角进行转换过程，通常是先原始欧拉角转换为矩阵，再从矩阵 转换为目标欧拉角

欧拉角围绕体轴旋转，因此给定步骤的旋转轴取决于先前旋转中使用的角度。在固定轴系统中，旋转轴始终相同，使用的都是直立轴。只要旋转以相反的顺序执行，这两个系统就是等效的。

固定轴约定也称为外旋（Extrinsic Rotation），而典型的欧拉角约定则被称为内旋（Intrinsic Rotation）。

在计算机图形学中，通常使用右手坐标系来描述物体的旋转，其中规定了三个固定轴，分别是X轴、Y轴和Z轴。这三个轴的方向分别如下：

• X轴：向右
• Y轴：向上
• Z轴：指向观察者的方向

这种约定被称为右手定则，其中X轴和Y轴组成了平面坐标系，而Z轴则是垂直于平面坐标系的轴，被称为深度轴或Z轴。

在使用固定轴进行物体的旋转时，通常是绕着X轴、Y轴和Z轴进行旋转，例如，绕X轴进行旋转时，就是绕着从物体中心向右的轴进行旋转。在进行旋转时，旋转轴的方向是不变的，只有旋转的角度和旋转的方向才会改变。

在图形学中，固定轴约定是非常重要的，因为它可以确保物体的旋转方向和角度是一致的，从而实现更精确的旋转效果。同时，在3D建模、动画制作等领域中，固定轴也是非常常用的一种工具。

---

欧拉角是一种用于描述物体在三维空间中旋转的数学工具，在计算机图形学中被广泛应用。欧拉角的约定有很多种，常用的约定包括以下三种：

1. XYZ欧拉角约定：这种约定通常被用于飞机、船舶等需要绕多个轴进行旋转的物体。在这种约定中，物体首先绕X轴旋转一定角度，然后再绕Y轴旋转一定角度，最后绕Z轴旋转一定角度。
2. ZYX欧拉角约定：这种约定通常被用于机器人、飞行器等需要绕多个轴进行旋转的物体。在这种约定中，物体首先绕Z轴旋转一定角度，然后再绕Y轴旋转一定角度，最后绕X轴旋转一定角度。
3. YXZ欧拉角约定：这种约定通常被用于物体的相机视角等需要以某一轴为基准进行旋转的情况。在这种约定中，物体首先绕Y轴旋转一定角度，然后再绕X轴旋转一定角度，最后绕Z轴旋转一定角度。

以上三种欧拉角约定都是常用的约定方式，但不同的约定方式可能会影响旋转顺序和旋转结果。因此，在使用欧拉角进行物体旋转时，需要根据实际需要选择合适的欧拉角约定，以保证旋转结果的正确性。

¶8.3.3 欧拉角的优点

欧拉角仅使用3个数字来表示设置定向的参数。它与其他形式表示定向的优势如下：

1. 欧拉角更易于人类使用。它符合人类直观表述的思考或想象。当一个定向需要以数字方式显示或通过键盘输入时，欧拉角确实时唯一的选择。
2. 欧拉角使用尽可能小的表示。欧拉角使用3个数字来表述定向，没有任何其他系统可以使用少于3个数字来设置三维定向的参数。
3. 任意一组3个数字都是有效的。没有一组无效的欧拉角。

¶8.3.4 欧拉角的缺点

缺点主要包括：

1. 给定定向的表示不是唯一的。存在别名现象。
2. 两个定向之间的插值是有问题的。
3. 存在万向节死锁。

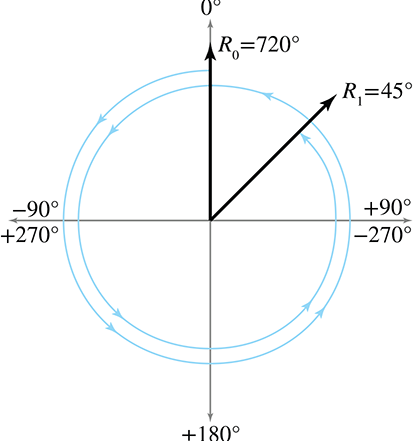
第一个别名问题，一是因为所有角度都可以加上$360^{\circ}$保持不变，第二个原因是因为绕着三个轴的旋转并非完全相同独立，如俯仰角向下旋转$135^{\circ}$与先通过航向角旋转$180^{\circ}$，再旋转俯仰$45^{\circ}$，最后滚转角旋转$180^{\circ}$的结果是一样的。为了处理球面坐标的别名，我们建立规范集。任何给定点再规范集中都具有唯一的表示。欧拉角可以使用类似的技术。我们将航向角和滚转角限制为$(-180^{\circ}, +180^{\circ}]$并将俯仰角限制为$[-90^{\circ},+90^{\circ}]$。但这样还存在一个歧义性，当pitch角度是$\pm 90^{\circ}$时，heading和bank旋转是一样的效果，这个现象称为万向锁（Gimbal Lock）。在这种情况下，定义变换的轴是heading，bank轴始终为0。因此欧拉角的标准坐标规则为：

$$\left\{\begin{aligned} -180^{\circ}<& h \leq 180^{\circ} \\ -90^{\circ} \leq & p \leq 90^{\circ} \\ -180^{\circ}<b & \leq 180^{\circ} \\ p=\pm 90^{\circ} & \Rightarrow \quad b=0 \end{aligned}\right.$$

当通过代码实现欧拉角时，最好保证返回的数值时标准坐标。

别名问题表述如下图：

第二个问题是关于角度变换插值的。 插值变换是指，有两个角度$\mathbf{R}_{0}$和$\mathbf{R}_{1}$，希望通过参数$0 \leq t \leq 1$，实现$\mathbf{R}(t)$在$\mathbf{R}_{0}$ 和 $\mathbf{R}_{1}$间线性变化。标准线性插值公式（lerp）独立应用于3个角度中的每一个，如下表示：

$$\begin{aligned} \Delta \theta &=\theta_{1}-\theta_{0} \\ \theta_{t} &=\theta_{0}+t \Delta \theta \end{aligned}$$

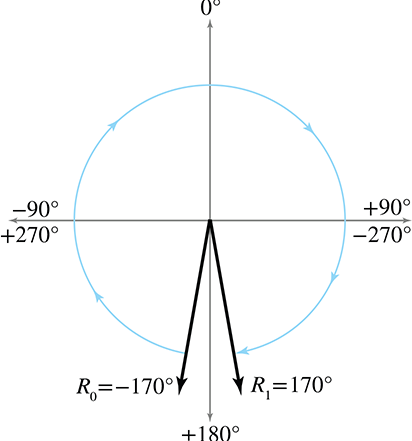
即使规范角度也不能完全解决问题。由于旋转角度的循环特性，可能发生第二类插值问题。假设$h_0=-170^{\circ}$且$h_1=170^{\circ}$，它们都属于规范值（都在$(-180^{\circ},+180^{\circ}]$区间内），这两个航向值实际相差仅$20^{\circ}$，但原生插值无法正常工作，因为它将顺时针旋转$340^{\circ}$，而不是采用较短的逆时针旋转$20^{\circ}$。如下图所示：

第二类问题的解决方案是将插值方程中使用的角度之间的差异性限制在$(-180^{\circ},+180^{\circ}]$区间内以找到最短的弧。为此，可以引入以下表示法：

$$\mathbf{wrapPi}(x)=x-360^{\circ}\left\lfloor\left(x+180^{\circ}\right) / 360^{\circ}\right\rfloor$$

其中，$\lfloor \cdot \rfloor$表示floor函数（向下取整函数）。

回归欧拉角，使用$\mathbf{wrapPi}$函数可以在两个角度之间插值时轻松获取最短弧度，具体如下：

$$\begin{align} \Delta\theta &=\mathbf{wrapPi}(\theta_1-\theta_2), \\ \theta_t&=\theta_0+t\theta\Delta\theta \end{align}$$

第三个问题万向锁无法被解决。只要使用了三个数值来表达旋转，那么当第二个轴旋转至$90^{\circ}$时，第一个轴与第三个轴的旋转效果都会变得相同。

¶8.3.5 欧拉角小结

1. 欧拉角使用了3个角度值存储定向。这些角度值时围绕3个对象空间轴的有序旋转。
2. 最常见的欧拉角系统是航向-俯仰-滚转（Heading-Pitch-Bank）系统。航向角和俯仰角表示物体朝向那个方向——航向给出“罗盘读数”，俯仰角测量偏斜角，而滚转角则测量“扭转”的量。
3. 在固定轴系统中，这些旋转将围绕直立轴而不是移动的体轴。该系统和欧拉角是一样的，前提是我们以相反的顺序执行旋转。
4. 在使用欧拉角时最好不要依赖术语。应始终确保你获得精确的工作定义。
5. 在大多数情况下，与其他表示定向的方法相比，欧拉角对于人类来说更直观。
6. 当内存有限时，欧拉角使用可接受的最小数据量来存储三维定向，而且欧拉角比四元数更容易压缩。
7. 没有一组无效的欧拉角。任何3个数字都有一个有意义的解释。
8. 由于旋转角度的循环性质，并且旋转不是完全独立的，因此欧拉角会出现别名问题。
9. 使用规范的欧拉角可以简化欧拉角上的许多基本查询。如果航向角和滚转角在$(-180^{\circ},+180^{\circ}]$区间内，则该欧拉角三元组在规范集合中。此外，如果俯仰角是$\pm90^{\circ}$，则滚转角是零。
10. 当俯仰角为$\pm90^{\circ}$时，会发生万向节死锁。在这种情况下，由于航向和滚转角都围绕垂直轴旋转，因此对象会失去一个自由度。
11. 三维中的任何定向都可以通过使用欧拉角来表示，我们可以在规范集中对该定向的唯一表示达成一致。
12. $\mathbf{wrapPi}$函数时一个非常方便的工具，她简化了我们必须处理角度循环特性的情况。这种情况在实践中经常出现，特别时在欧拉角的背景下，但在其他时候也是如此。
13. 别名的简单形式固然令人恼火，但是有一些解决方法。万向节死锁时一个更基本性的问题，没有简单的解决方案。万向节死锁之所以时一个问题，因为定向的参数空间具有不连续性。这意味着定向的微小彼岸花可能导致各个角度的很大变换。使用欧拉角的定向之间的插值可能会变得很怪异或采取摇摆不定的路径。

¶8.4 轴-角和指数映射表示方式

欧拉还提出了欧拉旋转理论（Euler‘s rotation theorem）：任何的3D旋转，都可以通过绕着某一个轴的单一旋转实现。如给定了两个旋转$\mathbf{R}_1和\mathbf{R}_2$，存在一个轴$\hat{\mathbf{n}}$，使得$\mathbf{R}_1和\mathbf{R}_2$两个旋转的结合可以通过绕着$\hat{\mathbf{n}}$轴的一次旋转搞定。

这种通过轴$\hat{\mathbf{n}}$和一个旋转角度$\theta$来表示的方法称为轴角法（Axis-Angle）。

而指数映射法(exponential map)是更进一步，通过$\mathbf{e}=\theta \hat{\mathbf{n}}$将轴和角结合在一起表示。如果想获取角度，可以通过$\theta=\|\mathbf{e}\|$。如果想获取旋转轴，可以对$\mathbf{e}$进行归一化，即$\hat{\mathbf{n}}=\bar{\mathbf{e}}$。

当$\theta=0$时，轴角法会出现歧义性，但是指数映射法不会（因为最终值已经变为了0）.同样，因为角度和轴的正负号造成的别名问题，指数映射法中也不会发生，因为正负号被相乘的操作抵消了。

但是因为加减$360^{\circ}$造成的别名问题，无论是轴角法还是指数映射法中都会出现。

同时，在使用指数映射法的时候，多个角度的旋转不能通过加法来获得。因为加法操作是支持交换律的，而旋转操作不支持。

如有两个旋转$\mathbf{e}_{1}=\left[90^{\circ}, 0,0\right]$和$\mathbf{e}_{2}=\left[0,90^{\circ}, 0\right]$，先执行$\mathbf{e}_{1}$和先执行$\mathbf{e}_{2}$的结果是不同的。因为旋转轴都是针对于物体坐标的，后者的旋转轴位置会受前一个旋转的影响。

但是这个结果的差距会随着角度的缩小而缩小，如旋转的角度是2°的话，那么结果的差异相对来说没有那么明显。因此一定意义上如果旋转的角度足够小，那么可以通过指数映射法的加法来结合角度的旋转。

轴角法更多的是一个概念上的方法，在实际上中运用的比较少。四元数实际上是通过轴角法演变来的。

指数映射法运用的相对较多。在计算角速度的时候，通常使用指数映射法。一是因为指数映射法受加减360°别名的影响，因此可以保留速度的变换。二是因为虽然指数映射法的加法无法完美结合多个变换，但是可以结合多个变换的变换角度的大小。

¶8.5 四元数

可先阅读此文章：Understanding Quaternions 中文翻译《理解四元数》 (qiujiawei.com)

四元数通过使用4个数字来表示定向以避免万向节死锁，这也是“四元数”名称的由来。

¶8.5.1 四元数表示法

四元数包含标量分量和三维向量分量。通常将标量分量称为$w$。我们可以将向量分量称为单一的实体$\mathbf{v}$或单个分量$x、y和z$。以下是两种表示法的实例：

$$\begin{bmatrix} w & \mathbf{v} \end{bmatrix} \quad\quad \begin{bmatrix} w & (x & y & z) \end{bmatrix}$$

也可以垂直编写扩展四元数，因为四元数的“行”和“列”形式之间没有显著的区别，只是书写美观目的的选择。垂直编写如下所示：

$$\begin{bmatrix} w \\ \left( \begin{matrix} x \\ y \\ z \end{matrix} \right) \end{bmatrix}$$

¶8.5.2 这4个数字的意思

之前提到了轴角法表示旋转，即通过$(\theta, \hat{\mathbf{n}})$表达旋转。可以将其表示为四元数，将其中的旋转角度和旋转轴的信息进行编码放入四个数中，如下所示：

$$\begin{aligned} \begin{bmatrix} w & \mathbf{v} \end{bmatrix} &= \begin{bmatrix} \cos (\theta / 2) & \sin (\theta / 2) \hat{\mathbf{n}} \end{bmatrix} \\ \begin{bmatrix} w & (x & y & z \end{bmatrix} &= \begin{bmatrix} \cos (\theta / 2) & (\sin (\theta / 2) n_{x} & \sin (\theta / 2) n_{y} & \sin (\theta / 2) n_{z})\end{bmatrix} \end{aligned}$$

这样的四元数是关于角度旋转的，其中的$\mathbf{v}$和旋转轴$\hat{\mathbf{n}}$相关，$w$和旋转角度$\theta$相关。

¶8.5.3 四元数变负

四元数可以变负，其完成的方式很简单，就是让每个分量变负，其公式如下：

$$\begin{align} -\mathbf{q} &=-\begin{bmatrix} w & (x & y & z)\end{bmatrix}=\begin{bmatrix} -w & (-x & -y & -z)\end{bmatrix} \\ &= - \begin{bmatrix} w & v\end{bmatrix} = \begin{bmatrix} -w & -v\end{bmatrix} \end{align}$$

关于四元数变负的一个令人惊讶的事实是，它确实没有做任何事情，至少角度位置的情况下是如此。三维中的任何角度位移在四元数格式中具有恰好不同的两个表示，并且它们是彼此的负数。

如果将360添加到$\theta$，那么它将不会改变$\mathbf{q}$表示的角位移，但它会使$\mathbf{q}$得所有4个分量均变负。

¶8.5.4 单位四元数

在几何学上，有两个单位四元数代表“没有角度位移”。它们是：

$$\begin{bmatrix}1 & \mathbf{0}\end{bmatrix} \quad 和 \quad \begin{bmatrix}-1 & \mathbf{0}\end{bmatrix}$$

这里的$\mathbf{0}$代表着零向量。当$\theta$是$360^{\circ}$的偶数倍时，则$\cos{\theta/2}=1$，我们有第一种形式。当$\theta$是$360^{\circ}$的奇数倍时，则$\cos{\theta/2}=-1$，我们有第二种形式。这两种情况下，$\sin{\theta/2}=0$，因此$\hat{\mathbf{n}}$的值是无关紧要的。

在数学中，$\mathbf{q}$和$\mathbf{-1}$并不相等，因此$\begin{bmatrix} -1 & \mathbf{0} \end{bmatrix}$不是一个真实的单位四元数。

¶8.5.5 四元数的大小

计算四元数的大小就像计算矢量和复数的一样。

$$\begin{align} ||\mathbf{q}|| &= ||\ \begin{bmatrix} w & (x & y &z) \end{bmatrix}\ ||=\sqrt{w^2+x^2+y^2+z^2} \\ &= ||\ \begin{bmatrix} w & \mathbf{v}\end{bmatrix}\ || = \sqrt{w^2 + ||v||^2} \end{align}$$

对于旋转四元数来说：

$$\begin{align} ||\mathbf{q}|| &= ||\ \begin{bmatrix} w & \mathbf{v} \end{bmatrix}\ ||= \sqrt{w^2+||v||^2} \\ &=\sqrt{\cos^2({\theta/2)} + (\sin(\theta/2)||\hat{\mathbf{n}}||)^2} && (使用\theta和\hat{\mathbf{n}}代入)\\ &=\sqrt{\cos^2(\theta/2) + \sin^2({\theta/2})||\hat{\mathbf{n}}||^2 } \\ &=\sqrt{\cos^2(\theta/2) + \sin^2({\theta/2})(1) } && (\hat{\mathbf{n}}是一个单位向量)\\ &=\sqrt{1} && (\sin^2{x} + \cos^2{x} = 1)\\ &=1 \end{align}$$

¶8.5.6 四元数的共轭和逆

四元数的共轭（Conjugate）表示为$\mathbf{q^{*}}$，是通过四元数的向量部分变负得到的。公式如下:

$$\begin{align} \mathbf{q^{*}} &= \begin{bmatrix} w & \mathbf{v} \end{bmatrix}^{*} = \begin{bmatrix} w & \mathbf{-v} \end{bmatrix} \\ &= \begin{bmatrix} w & (x & y &z) \end{bmatrix}^{*} = \begin{bmatrix} w & (-x & -y & -z)\end{bmatrix} \end{align}$$

四元数的逆（Inverse）表示为$\mathbf{q^{-1}}$，定义为四元数除以其大小的共轭。公式如下：

$$\mathbf{q^{-1}}=\frac{\mathbf{q^{*}}}{||\mathbf{q}||}$$

单位四元数的逆与实数（标量）的倒数的关系：

$$\mathbf{qq^{-1}}=\begin{bmatrix}1 & \mathbf{0}\end{bmatrix}$$

因为$\hat{\mathbf{n}}$和$-\hat{\mathbf{n}}$是平行的，所以$\mathbf{q}$和$\mathbf{q^*}$表示相反的角位移。从几何意义上来说，用于旋转的四元数，因为模为1，所以$\mathbf{q}^{*}=\mathbf{q}^{-1}$。它们都表示为绕着相反的轴（因为$\mathbf{v}$取反了）进行旋转。

¶8.5.7 四元数乘法

四元数可以相乘，其结果类似于向量的叉积，它将产生一个新的四元数，并且它不是可交换的。公式如下：

$$\begin{align} \mathbf{q_1q_2} &= \begin{bmatrix} w_1 & (x_1 & y_1 & z_1)\end{bmatrix} \begin{bmatrix}w_2 & (x_2 & y_2 & z_2) \end{bmatrix} \\ &= \begin{bmatrix}w_1w_2 - x_1x_2 - y_1y_2 - z_1z_2 \\ \left( \begin{matrix} w_1x_2 + x_1w_2 + y_1z_2 - z_1y_2 \\ w_1y_2 + y_1w_2 + z_1x_2 - x_1z_2 \\ w_1z_2 + z_1w_2 + x_1y_2 - y_1x_2 \end{matrix} \right) \end{bmatrix} \\ &= \begin{bmatrix} w_1 & \mathbf{v_1} \end{bmatrix} \begin{bmatrix} w_2 & \mathbf{v_2} \end{bmatrix} \\ &= \begin{bmatrix} w_1w_2 - \mathbf{v_1 \cdot v_2} & w_1\mathbf{v_2} + w_2\mathbf{v_1} + \mathbf{v_1} \times \mathbf{v_2} \end{bmatrix} \end{align}$$

四元数的积也成为哈密尔顿积（Hamilton Product）。由公式可推导出一下几个属性：

• 四元数乘法是可结合的，但不是可交换的：

$$\mathbf{(ab)c=a(bc)} \\ \mathbf{ab \neq ba}$$

• 四元数乘积的大小等于它们的大小的乘积：

$$||\mathbf{q_1q_2}|| = ||\mathbf{q_1}||\ ||\mathbf{q_2}||$$

• 四元数乘积的倒数等于以相反顺序取的倒数的乘积：

$$\begin{align} \mathbf{(ab)^{-1}} &= \mathbf{b^{-1}a^{-1}} \\ \mathbf{q_1q_2 \cdots q_{n-1}q_n} &= \mathbf{q_n^{-1} q_{n-1}^{-1} \cdots q_2^{-1}q_1^{-1}} \end{align}$$

• 使用四元数乘法来旋转三位向量。定义一个四元数$\mathbf{p}=\begin{bmatrix}0&(x&y&z)\end{bmatrix}$，设$\mathbf{q}$是讨论过的$\begin{bmatrix}\cos{\theta/2} & \hat{\mathbf{n}}\sin{\theta/2}\end{bmatrix}$,其中$\hat{\mathbf{n}}$是单位向量旋转轴，$\theta$是旋转角。则有：

$$\mathbf{p^{'}=qpq^{-1}}$$

• 四元数乘法可以用于连续多个旋转，就像矩阵乘法一样：

$$\begin{align} \mathbf{q^{'}} & = \mathbf{b(apa^{-1})b^{-1}} \\ &= \mathbf{(ba)p(a^{-1}b^{-1})} \\ &= \mathbf{(ba)p(ba)^{-1}} \end{align}$$

¶8.5.8 四元数的“差”

要计算两个四元数之间的差值，需要使用四元数的乘法和倒数。“差”意味着从一个反向到另一个方向的角位移。

给定方向$\mathbf{a}$和$\mathbf{b}$，可以计算从$\mathbf{a}$到$\mathbf{b}$旋转的角位移$\mathbf{d}$，表示为$\mathbf{da=b}$。四元数乘法从右到左执行旋转。

$$\begin{align} \mathbf{(da)a^{-1}} &= \mathbf{ba^{-1}}, \\ \mathbf{d(aa^{-1})} &= \mathbf{ba^{-1}}, \\ \mathbf{d} \begin{bmatrix}1 & 0\end{bmatrix} &= \mathbf{ba^{-1}}, \\ \mathbf{d} &= \mathbf{ba^{-1}} \end{align}$$

¶8.5.9 四元数点积

点积运算是为四元数定义的。它的表示法和向量点积非常相似，结果是标量。表示如下：

$$\begin{align} \mathbf{q_1 \cdot q_2} &= \begin{bmatrix}w_1 & \mathbf{v_1} \end{bmatrix}\cdot\begin{bmatrix}w_2 & \mathbf{b_2}\end{bmatrix} \\ &= w_1w_2 + \mathbf{v_1 \cdot v_2} \\ &= \begin{bmatrix}w_2 & (x_1 & y_1 & z_1)\end{bmatrix} \cdot \begin{bmatrix}w_2 & (x_2 & y_2 & z_2)\end{bmatrix} \\ &= w_1w_2 + x_1x_2 + y_1y_2 + z_1z_2 \end{align}$$

在上一节求四元数差值的部分中，如果设$\mathbf{a}=[w_1 \quad \mathbf{v_1}]$和$\mathbf{b}=[w_2 \quad \mathbf{v_2} ]$，那么$\mathbf{d}$中的$\omega$部分即为$w_1 w_2+\mathbf{v_1} \cdot \mathbf{v_2}$，即和$\mathbf{a} \cdot \mathbf{b}$的结果相同。

$$\begin{align} \mathbf{d} &= \mathbf{ba^{-1}} \\ \mathbf{d} &= \mathbf{ba^{*}} \quad(单位四元数:\mathbf{q}^{*}=\mathbf{q}^{-1}) \\ \mathbf{d} &= \begin{bmatrix} w_1w_2 + \mathbf{v_1 \cdot v_2} & w_1\mathbf{v_2} - w_2\mathbf{v_1} - \mathbf{v_1} \times \mathbf{v_2} \end{bmatrix} \\ \mathbf{d} &= \begin{bmatrix} w & \mathbf{v_d} \end{bmatrix}, \\ w &=w_1 w_2+\mathbf{v_1} \cdot \mathbf{v_2} \end{align}$$

¶8.5.10 四元数的对数、指数和标量乘法

为了书写方便，四元数可表示为，$\alpha=\theta / 2，\mathbf{q}=[\cos \alpha \quad \hat{\mathbf{n}} \sin \alpha]$。

$\mathbf{q}$的对数可定义为：$\log\mathbf{q}=\log\left([\cos\alpha \quad \hat{\mathbf{n}}\sin{\alpha}]\right)\equiv [0 \quad \alpha\hat{\mathbf{n}}]$。

定义$\mathbf{p}=\begin{bmatrix}0 & \alpha\hat{\mathbf{n}}\end{bmatrix},||\hat{\mathbf{n}}||=1$。则有四元数的指数函数如下：

$$\exp{\mathbf{p}}=\exp{(\begin{bmatrix}0 & \alpha\hat{\mathbf{n}}\end{bmatrix})}\equiv\begin{bmatrix}\cos{\alpha} & \hat{\mathbf{n}}\sin{\alpha}\end{bmatrix}$$

四元数对数和指数与它们的标量类似物有关。对于任意标量$a$，有$e^{\ln{a}=a}$。同样四元数$\exp$函数定义为四元数对数的逆，即：

$$\exp{\log{\mathbf{q}}}=\mathbf{q}$$

四元数与标量相乘：

$$k\mathbf{q}=k\begin{bmatrix}w & \mathbf{v}\end{bmatrix}=\begin{bmatrix}kw & k\mathbf{v}\end{bmatrix}$$

¶8.5.11 四元数指数

四元数的指数形式（Exponentiation），写为$\mathbf{q}^{t}$

在自然数中，$a^0=1,a^1=a$，即指数从$0\sim1$变化的过程中，结果从$1\sim a$逐渐变换。在四元数中类似，即指数从$0\sim 1$的过程中，结果从$[1 \quad \mathbf{0}]$逐渐变换为$\mathbf{q}$。要计算表示四元数$\mathbf{q}$表示角位移的三分之一的四元数，可以计算$\mathbf{q^{1/3}}$。

四元数指数操作的几何意义在于，它可以截取或倍化差值，因为：

上式中，先进行了 log 操作，由上节可知，log 操作的结果是将角度抽离出来（从$\sin \alpha \hat{\mathbf{n}}$变为了$\alpha \hat{\mathbf{n}}$）。这时候乘以$t$就是直接对角度进行截取或倍化。然后进行的 exp 操作，则又是将角度变化回了四元数。

所以如果$\mathbf{q}$表示绕着 x 轴旋转 30°，那么$\mathbf{q}^2$表示绕着 x 轴旋转 60°，$\mathbf{q}^{-1/3}$表示绕着反方向旋转了 10°。

但是指数操作的旋转的结果是最短路径，即$\mathbf{q}^8$的结果并不是旋转 240°，而是 120°。

另外四元数的几何操作不满足实数的指数操作的一些性质，如$\left(a^{s}\right)^{t}=a^{s t}$无法在四元数中实现。

四元数的取幂公式：

$$\mathbf{q^{t}}=\exp(t\log\mathbf{q})$$

四元数指数计算代码

// 四元数（输入和输出）
float w,x,y,z;

// 输入指数
float exponent;

// 检查单位四元数的情况，此步骤可以防止除以零
if (fabs(w) < .9999f) {
    // 提取半角alpha (alpha = theta/2)
    float alpha = acos(w);

    // 计算新alpha值
    float newAlpha = alpha * exponent;

    // 计算行w值
    w = cos(newAlpha);

    // 计算新的xyz值
    float mult = sin(newAlpha) / sin(alpha);
    x *= mult;
    y *= mult;
    z *= mult;
}

¶8.5.12 四元数插值

Slerp运算，它代表的是球面线性插值（Spherical Linear Interpolation）。Slerp允许在两个定向之间平滑插值，它可以避免困扰欧拉角插值的所有问题。

如果在两个标量值$a_0$和$a_1$之间进行插值，则有标准线性插值（Linear Interpolation，Lerp）公式：

$$\begin{align} \Delta{a} &= a_1 - a_0, \\ lerp(a_0,a_1,t) &= a_0 + t\Delta{a} \end{align}$$

插值计算基本步骤：

1. 计算两个值之间的差值。
2. 取该差值的一部分。
3. 取原始值并按插值的这一部分进行调整。

Slerp的推导如下：

1. 插值计算（8.5.8节）。从$\mathbf{q_0}$到$\mathbf{q_1}$的角位移由下式给出：

$$\Delta = \mathbf{q_1q_0^{-1}}$$

2. 取插值的一部分（8.5.11节）。公式如下：

$$(\Delta{q})^{t}$$

3. 取原始值并按插值的这一部分进行调整。通过四元数乘法组合角位移来“调整”初始值，其实现方式如下：

$$(\Delta{q})^{t}q_0$$

则可推导出：

$$slerp(\mathbf{q_0},\mathbf{q_1},t)=(\mathbf{q_1q_0^{-1}})t\mathbf{q_0}$$

对球面线性插值进行平面可视化后，可得下图：

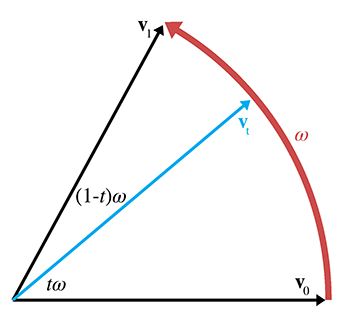
定义两个二维向量$\mathbf{v_0}$和$\mathbf{v_1}$，二者都是单位长度。我们希望计算$\mathbf{v_1}$的值，这是围绕弧进行平滑插值的结果，插值的计算是将从$\mathbf{v_0}$和$\mathbf{v_2}$的距离乘以因子$t$。如果设$\omega$是弧从$\mathbf{v_0}$到$\mathbf{v_1}$截取的角度，则$\mathbf{v_1}$是围绕该弧旋转$\mathbf{v_0}$(旋转角度为$t\omega$)的结果。

将$\mathbf{v_1}$（它将也是单位向量）表示为$\mathbf{v_0}$和$\mathbf{v_1}$的线性组合。换句话说，存在非负常数$k_0$和$k_1$，使得$\mathbf{v_t}=k_0\mathbf{v_0}+k_1\mathbf{v_1}$。如下图所示。

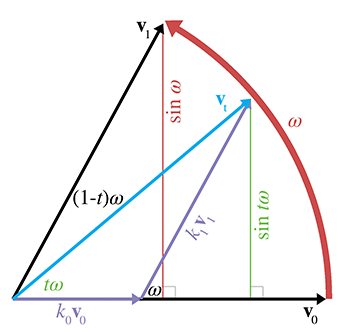
应用一些三角函数可得：

$$\begin{align} \sin{\omega} &= \frac{\sin{t\omega}}{k_1}, \\ k_1 &= \frac{\sin{t\omega}}{\sin{\omega}}, \\ k_0 &= \frac{\sin{(1-t)\omega}}{\sin\omega} \end{align}$$

由此，$\mathbf{v_t}$可以表示为：

$$\mathbf{v_t}=k_0\mathbf{v_0}+k_1\mathbf{v_1}=\frac{\sin{(1-t)\omega}}{\sin\omega}\mathbf{v_0}+\frac{\sin{t\omega}}{\sin{\omega}}\mathbf{v_1}$$

基本思路扩展到四元数空间中，可以将Slerp公式重新编写为：

$$slerp(\mathbf{q_0},\mathbf{q_1},t)=\frac{\sin{(1-t)\omega}}{\sin\omega}\mathbf{q_0}+\frac{\sin{t\omega}}{\sin{\omega}}\mathbf{q_1}$$

计算四元数Slerp代码实现：

// 两个输入四元数
float w0,x0,y0,z0;
float w1,x1,y1,z1;

// 插值参数
float t;

// 要计算的输出四元数
float w,x,y,z;

// 使用点积计算，四元数之间的“角度的余弦”
float cosOmega = w0*w1 + x0*x1 + y0*y1 + z0*z1;

// 如果点积为负，则将其中一个输入的四元数变负，以取得最短思维的“弧”
if (cosOmega < 0.0f) {
    w1 = -w1;
    x1 = -x1;
    y1 = -y1;
    z1 = -z1;
    cosOmega = -cosOmega;
}

// 检查它们是否靠得非常近，以避免出现除以零的问题
float k0, k1;
if (cosOmega > 0.9999f) {
    // 如果靠得非常近，则仅使用线性插值
    k0 = 1.0f-t;
    k1 = t;
} else {
	// 使用三角函数恒等式 sin^2(omega)+cos^2(omega) = 1
    // 计算角度的正弦
    float sinOmega = sqrt(1.0f - cosOmega*cosOmega);

    // 通过sine和cosine值计算角度
    float omega = atan2(sinOmega, cosOmega);

	// 计算分母的倒数，因此只需要除以一次即可
    float oneOverSinOmega = 1.0f / sinOmega;

	// 计算插值参数
    k0 = sin((1.0f - t) * omega) * oneOverSinOmega;
    k1 = sin(t * omega) * oneOverSinOmega;
}

// 插值
w = w0*k0 + w1*k1;
x = x0*k0 + x1*k1;
y = y0*k0 + y1*k1;
z = z0*k0 + z1*k1;

¶8.5.13 四元数的优缺点

• 优点：

1. 平滑插值。Slerp插值方法提供了定向之间的平滑插值。没有其他表示方法能提供这样的平滑插值。
2. 角位移快速连接和逆。我们可以通过使用四元数叉积将一系列角位移连接成单个角位移。使用矩阵的相同运算涉及更多的标量运算，因为单指令多数据（Single Instruction Multiple Data，SIMD）向量运算可以非常快速的执行矩阵乘法。四元数共轭提供了一种非常有效地计算相反角位移的方法。这可以通过转置旋转矩阵来完成，但是对于欧拉角来说并不容易。
3. 矩阵形式的快速转换。四元数可以快速地与矩阵形式相互转换，并且其转换速度比欧拉角更快一些。
4. 只有4个数字。由于四元数包含4个标量值，因此它比使用9个数字的矩阵更经济，但还是比欧拉角大33%。

• 缺点：

1. 略大于欧拉角。四元数使用4个数字，但欧拉角只使用3个数字。四元数内的值不是沿[-1,+1]区间均匀间隔的，这意味着即使方向是均匀间隔的，分量也不会平滑插值，这使得四元数比欧拉角或者指数映射更难以打包成定点数。
2. 可能无效。这可能因为错误的输入数据或者积累的浮点舍入错误而发生。可以通过规范化四元数来确保它具有单位大小来解决这个问题。
3. 人类很难使用。在矩阵、欧拉角和四元数这3种方式中，四元数是人类最难以直接使用的方法。

¶8.5.14 作为复数的四元数

这一节是用从复数的角度来描述四元数，从这个角度可以解释两个问题，一是为什么从旋转角度来看，四元数代表的是$\theta/2$而不是$\theta$，二是为什么用于旋转的表达式是$\mathbf{qvq^{-1}}$

首先实数可以通过矩阵形式进行表达，如实数$a$，可按如下方式表示：

复数同样可以通过矩阵形式表达，如复数$a+bi$，可以表达为：

而且这样表达复数，仍然可以满足$i^2=-1$的性质，如下

因为四元数的乘法是从右向左的，相当于是矩阵中的右手坐标系，所以矩阵中的每一列代表坐标轴，从上式可以看到，在$i$乘以$i$后，列从$[0,1]$变为了$[-1,0]$，从$[-1,0]$变为了$[0,-1]$，即旋转了 90°。

即可以将复数看作是一种旋转的表达，如果旋转$\theta^{\circ}$，即表达为：

这个矩阵即为之前在二维旋转中推导出的，旋转$\theta^{\delta}$的矩阵，只不过之前推导的是左手坐标系中的，这里是右手坐标系中的（两个坐标系的结果互为转置）。

如果将复数$x+yi$用矩阵表示为矩阵$[x,y]$，可以看到实数的乘法与矩阵的乘法同样可以对应起来。进一步证明可以通过实数来进行旋转操作。

同时复数的共轭，也可以与矩阵的求逆对应起来，两者都是进行逆变换。

当这个结论无法推导至三维空间中。在二维空间中，用实数和虚数$i$对应两个维度，但是在三维空间中无法用实数和两个虚数$i,j$来对应三个维度（无法用$3\times3$的矩阵表示）。

如果可以对应，那么三维的单位矩阵$I_3$，应该对应数字 1，三维的负单位矩阵$I_3$，应该对应-1。因为$i^2=-1$，所以表示虚数$i$的矩阵的平方应该等于$-I_3$。

但是$-I_3$的行列式值为-1，根据行列式性质“乘积的行列式等于行列式的乘积”，那么表示虚数$i$的矩阵的行列式的平方，应该等于-1，即该矩阵的行列式值为 i，这显然无法满足。

因此无法通过$3\times 3$的矩阵来表示三维三维的虚数。

数学家$William Hamilton$提出，可以通过四维的虚数来表示四维空间，即通过实数，和三个虚数$i,j,k$来表示。其中三个虚数满足：

而四元数就是一种形式的四维矩阵，即$[w,(x, y, z)]$可用来对应$w+x i+y j+z k$。

将四维的虚数用$4\times4$的矩阵表示有多个方法，以下为其中一种：

结合可得：

可以发现，$k$矩阵的左上部分与二维空间中$i$的表达一模一样，于是猜测$k$矩阵也可以用来表达旋转，且是绕着$z$的旋转。使用三维向量$[1,0,1]$来测试。该向量如果用四元数表达，则为$[0 \quad (1,0,1)]$，即用实数表达为$i+k$。因为是绕着$z$轴旋转，所以$z$的变量不会变，$xy$变量的结果与二维空间旋转结果相同，即最后的正确结果应该是$(\cos \theta,\sin\theta,1)$，即$\cos\theta i +\sin\theta j+k$
那么相乘过程可以表示为：

可以看到结果根本就不是一个三维空间中的向量，因为$w$参数并不为 0。这个结果中，$x,y$平面的答案是我们想要的，而$z,w$平面则不是。

如果对实数取共轭，即表达为$\cos\theta - k\sin \theta$，并且进行右乘，那么结果为：

结果仍然不是一个三维空间中你的向量，$x,y$平面的结果不变，$z,w$平面的结果虽然不同，但是与之前的结果正好相反，所以尝试将两个表达式结合在一起，即

与正确结果$\cos\theta i +\sin\theta j+k$相比，$\theta$变为了$2\theta$。因此如果要用复数来表达旋转的话，式子应该改为$(\cos \theta /2+k \sin \theta /2)(i+k)(\cos \theta /2-k \sin \theta /2)$，即四元数应该表达为$\mathbf{q}=[\cos \theta /2 \quad \mathbf{\sin \theta/2k}]$，且上述式子对应的乘法表达式为$\mathbf{qpq^-1}$。

而这就是前几节中定义的用四元数来表示乘法的方法。

¶8.5.15 四元数概要

1. 从概念上讲，四元数可以通过使用旋转轴和绕该轴旋转的量来表示角位移。
2. 四元数包含标量分量$w$和向量分量$\mathbf{v}$。它们与旋转角$\theta$和旋转轴$\hat{\mathbf{n}}$相关，并存在以下关系：$w=\cos(\theta/2),\mathbf{v}=\hat{\mathbf{n}}\sin(\theta/2)$。
3. 三位中的每个角位移在四元数中都有两个不同的表示，它们是相互的负数。
4. 表示“无角度位移”的单位四元数为$[1,\mathbf{0}]$。
5. 所有表示角位移的四元数都是“单位四元数”，其大小等于1。
6. 四元数的共轭表示相反的角位移。
7. 四元数乘法可用于将多个旋转连接成单个角位移。
8. 四元数取幂可用于计算角位移的倍数。
9. 四元数可以将被解释为四维复数。

¶8.6 方法比较

旋转方法	在坐标空间（对象和正立）之间旋转点	连续多次旋转	旋转的反转	插值	直接人类解释	存储效率	旋转的唯一表示	可能变得无效
矩阵	可能；通常可以通过 SIMD 指令高度优化。	可能；通常可以通过 SIMD 指令高度优化。注意矩阵蔓延问题。	使用矩阵转置易于快速。	极其有问题。	困难。	九个数字。	是。	正交矩阵中有六个度的冗余。可能会出现矩阵蔓延问题。
欧拉角	不可能（必须转换为旋转矩阵）。	不可能。	不易。	可能，但万向锁会导致怪异。	最容易。	三个数字，可以很容易地量化。	否，由于别名。	任何三个数字都可以无歧义地解释。
指数映射	不可能（必须转换为旋转矩阵）。	不可能。	使用向量取反易于快速。	可能，存在一些奇异点，但不像欧拉角那样麻烦。	非常困难。	三个数字，可以很容易地量化。	否，由于别名，但不像欧拉角那么复杂。	可能会出现误差累积问题。
四元数	在黑板上，是的。在计算机上实际上并不是很好。您最好将其转换为旋转矩阵。	可能。较少数量的标量操作比矩阵乘法，但可能不容易利用 SIMD 指令。注意误差蔓延问题。	使用四元数共轭易于快速。	Slerp 提供平滑的插值。	非常困难。	四个数字不能很好地量化；可以假定第四个分量始终为非负的并且四元数具有单位长度而将其减少到三个。	对于任何角位移，恰好有两个不同的表示，它们是彼此的相反数。	可能会出现误差蔓延问题。

---

引用：

1. Dunn, F. and Parberry, I. (2011). 3D math primer for graphics and game development $2^{nd}$.