3D数学基础：图形和游戏开发 读书笔记 第7章

笛卡尔积坐标不是精确绘制空间和定义位置的唯一系统。它的替代方案是极坐标系（Polar Coordinate System）。

¶7.1 关于二维极坐标空间

¶7.1.1 使用二维极坐标定位点

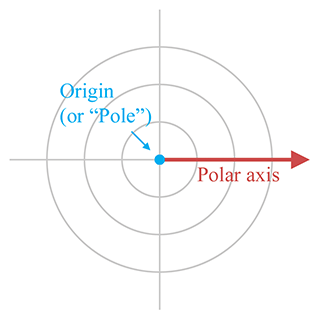
二维极坐标空间和笛卡尔积一样，也有一个原点，它叫做极点（Pole），但在轴上和笛卡尔积不同，它就一个轴，称为极轴（Polar Axis），它通常被描述为来自原点的射线。在数学上，极轴是指向右侧，因此它对应笛卡尔坐标中的$+x$轴，如下图所示：

笛卡尔坐标中，使用有符号距离$x、y$来描述一个二维点。而在极坐标中使用一个距离和一个角度来表示二维点。二维极坐标$(r,\theta)$指定二维空间中的点，$r$是半径，也表示从原点向前移动$r$个单位的距离；$\theta$是角度（也可以用弧度表示），它的正值通常被解释为逆时针旋转，负值解释为顺时针旋转。如下图表示：

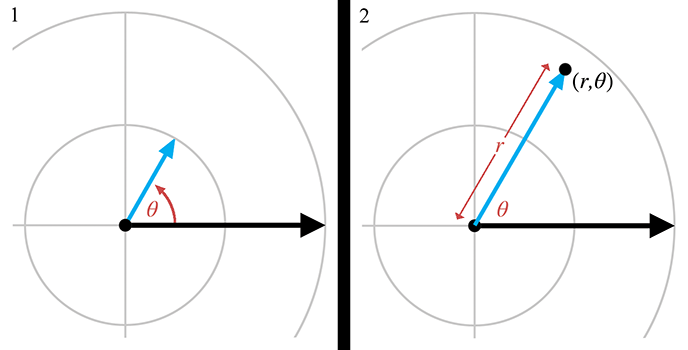
上图极坐标系图中的同心圆，表示$r$相同的点的集合，图中的直线则表示$\theta$相同的点的集合。

¶7.1.2 别名

在笛卡尔坐标系下，一个点只有一个表示。但是在极坐标系下，一个点有无数个表示。如过两个表示实际上是指同一个点，那么称这两个表示互为对方的别名（Aliasing）。

如果有点表示为$(r,\theta)$，那么所有它的别名可以表示为$((-1)^kr,\ \theta+k180^{\circ})$，其中$k$为任何整数。

极坐标中还有歧义性（singularity），即当$r=0$时，无论$\theta$取何值，结果都没有区别。

别名和歧义性本身并不会引发任何问题，只不过表达起来存在困难而已。对于极坐标来说，描述任何给定的“首选”方式称为该点的规范坐标（Canonical Coordinate）。如果$r$是非负的，并且在$(-180^{\circ},+180^{\circ}]$区间内，则二维极坐标对$(r,\theta)$在规范集内。如果原点直接朝“西”的点(x<0,y<0)，将使用$\theta=+180^{\circ}$。如果极坐标对$(r,\theta)$要在规范集中，则需要满足以下的三个条件：

$$f(x)= \begin{cases} r \geq 0 & 不会测量\textbf{向后}的距离 \\ -180^{\circ} < \theta \leq 180^{\circ} & 角度限制为1/2圈，使用+180^{\circ}代表朝\textbf{西} \\ r=0\ \Rightarrow\ \theta=0 & 在原点处，将角度设置为零 \end{cases}$$

可以通过以下方法将极坐标对$(r,\theta)$转换为其规范形式：

1. 如果$r=0$，则指定$\theta = 0$。
2. 如果$r <0$，则取反$r$，并向$\theta$加上$180^{\circ}$。
3. 如果$\theta \leq -180^{\circ}$,则将$360^{\circ}$加到$\theta$上，直到$\theta > -180^{\circ}$。
4. 如果$\theta > 180^{\circ}$，则从$\theta$减去$360^{\circ}$，直到$\theta \leq 180^{\circ}$。

¶7.1.3 关于二维中笛卡尔坐标和极坐标之间的变换

二维极坐标和笛卡尔坐标之间的变换示意图：

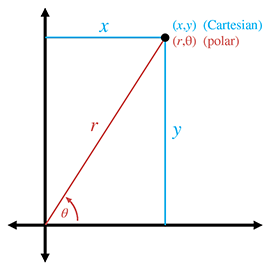
将极坐标对$(r,\theta)$变换为相应的笛卡尔坐标，可以用正弦和余弦得到以下定义：

$$x=r\cos\theta,\quad y=r\sin\theta$$

再由毕达哥拉斯定理可得$r=\sqrt{x^2+y^2}$。而$\theta$计算如下：

$$\begin{align} \frac{y}{x}&=\frac{r\sin\theta}{r\cos\theta},\\ \frac{y}{x}&=\tan\theta,\\ \quad\theta&=\arctan{(y/x)} \end{align}$$

但$\arctan{(y/x)}$的表达式存在两个问题，第一是当$x=0$时，表达式的除法是未定义的。第二是$\arctan$的范围为[−90∘,+90∘]。这个原因是$y/x$隐藏了一部分信息：和$x$和$y$分别存在正负，所以一共有4种组合，但是$y/x$却只有两个结果。直到这些则可以定义出新的函数$atan2$：

$$atan2(y,x)= \begin{cases} 0, & x=0,y=0 \\ +90^{\circ}, & x=0,y>0 \\ -90^{\circ}, & x=0,y<0 \\ arctan(y/x), & x > 0 \\ arctan(y/x)+180^{\circ}, & x<0,y\geq0 \\ arctan(y/x)-180^{\circ}, & x<0,y<0 \end{cases}$$

则有将二维笛卡尔坐标变换为极坐标公式：

$$r=\sqrt{x^2+y^2};\quad\quad \theta=atan2(y,x)$$

¶7.2 为什么会有人使用极坐标？

极坐标是一种表示平面上点位置的坐标系，它以点到原点的距离（称为极径）和点与极轴的夹角（称为极角）来描述点的位置。相对于直角坐标系，极坐标更适合描述圆形和环形结构，因为它们的对称性更明显。

以下是一些人们使用极坐标的原因：

1. 易于描述圆形结构：极坐标非常适合描述圆形结构，例如齿轮、风车、花瓣等。在这些情况下，使用极坐标可以使得坐标系更加简洁明了。
2. 易于计算极角和极径：在某些情况下，计算一个点的极坐标可能比计算它的直角坐标更加容易。例如，当你知道一个点在原点和另一个点之间的夹角和距离时，你可以更容易地计算出该点的极坐标。
3. 可以更好地可视化数据：在某些情况下，使用极坐标可以更好地可视化数据。例如，对于某些类型的数据，如温度、湿度等，你可以将这些数据表示为一个环形图，其中每个数据点代表一个角度和一个距离。

总的来说，极坐标是一种非常有用的工具，可以使得对于某些特定的问题和数据集更容易和更直观地理解和处理。

¶7.3 关于三维极坐标空间

二维的极坐标有两个坐标值了，那么在三维中添加第三个坐标值有两种选择，一种是添加一个线性距离（如$r$），这样我们会得到一个圆柱坐标（Cylindrical Coordinate）；另一种是添加一个角度（如$\theta$），这样我们将得到一个球面坐标（Spherical Coordinate）。

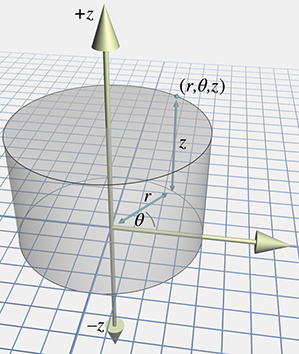
¶7.3.1 圆柱坐标

我们添加一个向上的$z$轴来表示圆柱坐标$(r,\theta,z)$。如图所示：

¶7.3.2 球面坐标

我们添加一个角度$\phi$来表示球面坐标$(r,\theta,\phi)$。如图所示：

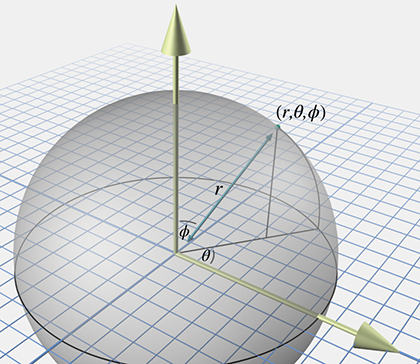
描述极坐标在三维中的点会进过一下几个步骤：

1. 首先站在原点，面向水平极轴的方向。垂直的指向是从脚指向头部。右臂向上，指向垂直极轴的方向。
2. 逆时针旋转角度$\theta$。
3. 将右臂向下旋转角度$\phi$。你的手臂现在指向极角$\theta$和$\phi$指定的方向。
4. 沿着右臂的方向从原点位移距离$r$。到达$(r,\theta,\phi)$所描述的点。

$\theta$被称为方位角（Azimuth），$\phi$被称为天顶角（Zenith）。在地球仪中经度（Longitude）对应的为$\theta$，维度（Latitude）对应的为$90^{\circ}-\phi$，海拔（Altitude）对应$r$。

¶7.3.3 在三维虚拟世界中有用的一些极坐标约定

之前章节描述的是数学层面上的极坐标系，但在3D游戏的使用中，数学层面的极坐标系存在以下问题：

• $\theta=0$的位置，对应$+x$方向，但是希望对应的反向是$+z$方向。
• $\phi=0$的位置，对应的是$+y$方向，但这样的话当$\phi=0$时，并不等于二维的极坐标系。而在$(r,\theta,90^{\circ})$时才等同于二维坐标系。
• $\theta$和$\phi$不方便记忆。

为此，3D游戏中的极坐标系做了如下改变

• 水平角度$\theta$命名为$h$(航向，heading)，且当$h=0$时指向$+z$方向。旋转正方向从$y$轴正方向看为顺时针。
• 垂直角度$\phi$命名为$p$(俯仰，pitch)，当$p=0$时，为水平角度，旋转正方向为向下。

3D游戏中的极坐标系如下图所示：

¶7.3.4 球面坐标的别名

三维坐标中同样存在别名和歧义性。

1. 当r取反时，$h+k180^{\circ}$，并且$p=-p$即能获得一样的值（别名）
2. 当$r=0$时，$h$和$p$取任意值都没有区别。（歧义性）
3. $(h,p)$可以表示为$(h\pm180^{\circ},180^{\circ}-p)$（别名） 如$h$向右转$90^{\circ}$，$p$向下转$45^{\circ}$，等同于$h$向左转$90^{\circ}$，$p$向下转$135^{\circ}$。
4. 当$p=\pm90^{\circ}$时，$h$取任意值没有区别（歧义性）（万向节死锁，gimbal lock）。

如同在二维中做的一样，我们可以定义一组规范的球形坐标。这样，三维空间中的任何点都可以映射到规范集合中的一个坐标三元组（Triple）。规范球面坐标需要满足以下条件：

$$\begin{cases} r\geq0&我们不会测量\textbf{向后}的距离 \\ -180^{\circ}<h\leq180^{\circ} & 航向限制为1/2圈。使用+180^{\circ}袋面朝南 \\ r=0\ \ \Rightarrow \ \ h=p=0 & 在原点处，将角度设置为零 \\ |p|=90^{\circ}\ \ \Rightarrow \ \ h=0 & 在直接向上或向下看时，设置航向为0 \end{cases}$$

可以通过以下方法将球面坐标$(r,h,p)$转换为其规范形式：

1. 如果$r=0$，则指定$h=p=0$。
2. 如果$r<0$，则将$r$变负，给$h$加$180^{\circ}$，并使$p$变负。
3. 如果$p<-90^{\circ}$，则给$p$加$360^{\circ}$，直到$p\geq-90^{\circ}$$。
4. 如果$p>270^{\circ}$，则给$p$减去$360^{\circ}$，直到$p\leq270^{\circ}$。
5. 如果$p>90^{\circ}$，则给$h$加$180^{\circ}$，直到$p=180^{\circ}-p$。
6. 如果$h\leq-190^{\circ}$，则给$h$加$360^{\circ}$，直到$h>-180^{\circ}$。
7. 如果$h>180^{\circ}$，则从$h$减去$360^{\circ}$，直到$h\leq180^{\circ}$。

¶7.3.5 球面坐标和笛卡尔坐标之间的转换

球坐标系与笛卡尔坐标系的转换图如下所示(数学表示)：

我们引进了一个新的变量$d$，它是点与垂直轴之间的水平距离。我们很容易得到:

$$d=r\sin\phi,\\ x=d\cos\theta=r\sin\phi\cos\theta,\quad y=d\sin\theta=r\sin\phi\sin\theta,\quad z=r\cos\phi$$

适用于3D游戏场景中的球面坐标则可以表示为：

$$x=r\cos{p}\sin{h},\quad y=-r\sin{p},\quad z=r\cos{p}\cos{h},\\-y/r=\sin{p}$$

则有笛卡尔坐标转换为球面坐标公式：

$$r=\sqrt{x^2+y^2+z^2};\quad h=atan2(x,z);\quad p=arcsin(-y/r)$$

¶7.4 使用极坐标指定向量

极坐标直接描述向量的两个关键属性——方向和长度。

---

引用：

1. Dunn, F. and Parberry, I. (2011). 3D math primer for graphics and game development $2^{nd}$.