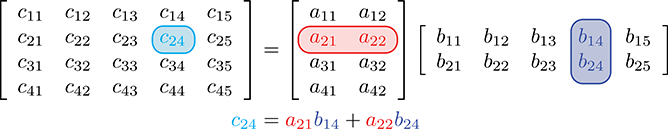3D数学基础：图形和游戏开发 读书笔记 第4章

矩阵在3D数学中具有根本意义上的重要性，它们主要用于描述连个坐标空间之间的关系。它们通过定义将向量从一个空间转换为另一个坐标空间来实现此目的。

¶4.1 矩阵的数学定义

¶4.1.1 矩阵维度和表示法

就向通过计算矩阵包含的数量来定义向量的维度一样，我们通过矩阵包含的行数和列数来定义矩阵的大小。我们将一个有r行，c列的矩阵称为r$\times$c矩阵。

4$\times$3矩阵

$$\begin{bmatrix} 4&0&12\\ -5&\sqrt{4}&3\\ 12&-\frac{4}{3}&-1\\ \frac{1}{2}&18&0 \end{bmatrix}$$

矩阵元素的下标表示法

$$\begin{bmatrix} m_{11}&m_{12}&m_{13}\\ m_{21}&m_{22}&m_{23}\\ m_{31}&m_{32}&m_{33} \end{bmatrix}$$

¶4.1.2 方形矩阵

具有相同行数和列数的矩阵称为方形矩阵。

• 对角元素与非对角元素：

下列矩阵中，加粗的$\mathbf{m_{11},m_{22},m_{33}}$属于对角元素，其他元素是非对角元素。

$$\begin{bmatrix} \mathbf{m_{11}}&m_{12}&m_{13}\\ m_{21}&\mathbf{m_{22}}&m_{23}\\ m_{31}&m_{32}&\mathbf{m_{33}} \end{bmatrix}$$

• 对角矩阵

如果矩阵中的所有非对角元素都为零，则该矩阵为对角矩阵。如下的4$\times$4对角矩阵。

$$\begin{bmatrix} 3&0&0&0\\ 0&1&0&0\\ 0&0&-5&0\\ 0&0&0&2\\ \end{bmatrix}$$

• 单位矩阵

矩阵乘法单位元素，是一个特殊的对角矩阵。维度为n的单位矩阵，表示为$\mathbf{I_{n}}$，是$n\times n$矩阵，其对角线上的值为1，其他元素值均为0.如下的三维单位矩阵。

$$\mathbf{I_{3}}= \begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix}$$

¶4.1.3 作为矩阵的向量

矩阵可以包含任何正数的行和列，包括一个。维数n的向量可以视为$1\times n$矩阵，我们称之为行向量（Row Vector），横向书写；也可以视为$n \times 1$矩阵，我们称之为列向量（Column Vector），纵向书写。从几何上来说，他们是相同的，大多数情况下，这种区分并不重要。书写表示如下。

$$\begin{bmatrix} 1&2&3 \end{bmatrix}, \begin{bmatrix} 4\\5\\6 \end{bmatrix}$$

¶4.1.4 矩阵转置

给定$r \times c$矩阵$\mathbf{M}$，$\mathbf{M}$的转置（Transpose）表示为$\mathbf{M^{T}}$,是$c \times r$矩阵，其中列由$\mathbf{M}$的行构成。看上去就是对角方式“翻转”，表现为$\mathbf{M_{rc}^T}=\mathbf{M_{cr}}$。

$$\begin{bmatrix} 1&2&3\\ 4&5&6\\ 7&8&9\\ 10&11&12 \end{bmatrix}^{T} = \begin{bmatrix} 1&4&7&10\\ 2&5&8&11\\ 3&6&9&12 \end{bmatrix}, \quad\quad \begin{bmatrix} a&b&c\\ e&e&f\\ g&h&i \end{bmatrix}^{T} = \begin{bmatrix} a&d&g\\ b&e&h\\ c&f&i \end{bmatrix}$$

对于向量，转置会将行向量转换为列向量，反之亦然，表述如下：

$$\begin{bmatrix} x&y&z \end{bmatrix}^{T} = \begin{bmatrix} x\\y\\z \end{bmatrix};\quad\quad \begin{bmatrix} x\\y\\z \end{bmatrix}^{T} = \begin{bmatrix} x&y&z \end{bmatrix}$$

1. 对于任何维度的矩阵$\mathbf{M}$，则$(\mathbf{M^{T}})^T=\mathbf{M}$。也就是，如果先转置矩阵，然后再转置一次，即可得到原始矩阵。此规则也适用于向量。
2. 任何对角矩阵$\mathbf{D}$等于其转置：$\mathbf{D^{T}=D}$。包括单位矩阵$\mathbf{I}$也是如此。

¶4.1.5 矩阵与标量相乘

矩阵$\mathbf{M}$可以与标量k相乘，得到与$\mathbf{M}$相同维度的矩阵。如下标量$4 \times s$矩阵的乘法表述：

$$k\mathbf{m}=k \begin{bmatrix} m_{11}&m_{12}&m_{13}\\ m_{21}&m_{22}&m_{23}\\ m_{31}&m_{32}&m_{33} \end{bmatrix} = \begin{bmatrix} km_{11}&km_{12}&km_{13}\\ km_{21}&km_{22}&km_{23}\\ km_{31}&km_{32}&km_{33} \end{bmatrix}$$

¶4.1.6 连个矩阵相乘

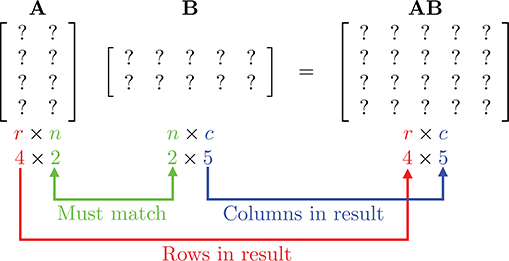
对于连个矩阵相乘，前者的列数必须与后者的行数相等。对于$r \times n$的矩阵$\mathbf{A}$，如果与$n \times c$的矩阵$\mathbf{B}$相乘，结果为$r \times c$的矩阵$\mathbf{AB}$。

矩阵乘法计算如下：设矩阵$\mathbf{C}$为$r \times n$矩阵$\mathbf{A}$与$n \times c$矩阵$\mathbf{B}$的$r \times c$乘积$\mathbf{AB}$。然后每个元素$c_{ij}$等于$\mathbf{A}$的行i与$\mathbf{B}$的列j的向量点积，其用计算公式表述如下：

$$c_{ij}=\sum_{k=1}^na_{ik}b_{kj}$$

计算$\mathbf{A}$的第2行和$\mathbf{B}$的第4列中元素的点积，示例如下：

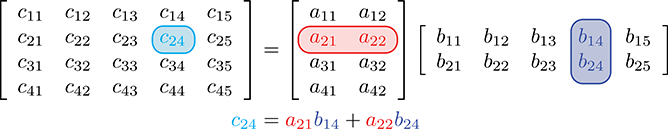
另一种助记法：

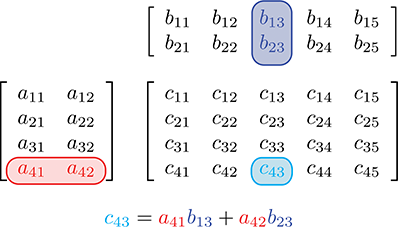
矩阵乘法公式如下：

$$\begin{align} \mathbf{AB} &= \begin{bmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{bmatrix} \begin{bmatrix} b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}\\ b_{31}&b_{32}&b_{33} \end{bmatrix} \\ &= \begin{bmatrix} a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31} & a_{11}b_{12}+a_{12}b_{22}+a_{13}b_{32} & a_{11}b_{13}+a_{12}b_{23}+a_{13}b_{33} \\ a_{21}b_{11}+a_{22}b_{21}+a_{23}b_{31} & a_{21}b_{12}+a_{22}b_{22}+a_{23}b_{32} & a_{21}b_{13}+a_{22}b_{23}+a_{23}b_{33} \\ a_{31}b_{11}+a_{32}b_{21}+a_{33}b_{31} & a_{31}b_{12}+a_{32}b_{22}+a_{33}b_{32} & a_{31}b_{13}+a_{32}b_{23}+a_{33}b_{33} \end{bmatrix} \end{align}$$

矩阵乘法需要注意的一些事项：

1. 将任何矩阵$\mathbf{M}$乘以一个方形矩阵$\mathbf{S}$（$\mathbf{S}$放那一边都可以，即$\mathbf{MS}$或$\mathbf{SM}$都行）将得到与$\mathbf{M}$大小相同的矩阵，条件是矩阵的大小允许乘法。如果$\mathbf{S}$是单位矩阵$\mathbf{I}$，则结果是原始矩阵$\mathbf{M}$。如：$\mathbf{MI=IM=M}$
2. 矩阵乘法不满足交换律：$\mathbf{AB\neq BA}$。
3. 矩阵乘法是满足结合律的：$\mathbf{(AB)C=A(BC)}$。
4. 矩阵乘法还可以与标量或向量结合：$(k\mathbf{A})B=k(\mathbf{AB})=\mathbf{A}(k\mathbf{B}),(v\mathbf{A})\mathbf{B}=v(\mathbf{AB})$。
5. 转置两个矩阵的乘积与以相反顺序取得其转置的乘积相同：$\mathbf{(AB)^T=B^T A^T}$。

¶4.1.7 向量与矩阵相乘

满足矩阵相乘规则(前者行与后者列相同)即可。三维行向量和列向量与$3 \times 3$的乘法如下：

$$\begin{align} & \begin{bmatrix}x&y&z\end{bmatrix} \begin{bmatrix} m_{11}&m_{12}&m_{13}\\ m_{21}&m_{22}&m_{23}\\ m_{31}&m_{32}&m_{33} \end{bmatrix}= \begin{bmatrix} xm_{11}+ym_{21}+zm_{31} & xm_{12}+ym_{22}+zm_{31} & xm_{13}+ym_{23}+zm_{33} \end{bmatrix} \\\\ & \begin{bmatrix} m_{11}&m_{12}&m_{13}\\ m_{21}&m_{22}&m_{23}\\ m_{31}&m_{32}&m_{33} \end{bmatrix} \begin{bmatrix}x\\y\\z\end{bmatrix} = \begin{bmatrix} xm_{11}+ym_{12}+zm_{13} \\ xm_{21}+ym_{22}+zm_{23} \\ xm_{31}+ym_{32}+zm_{33} \end{bmatrix} \\\\ & \begin{bmatrix} m_{11}&m_{12}&m_{13}\\ m_{21}&m_{22}&m_{23}\\ m_{31}&m_{32}&m_{33} \end{bmatrix} \begin{bmatrix}x&y&z\end{bmatrix} = (undefined) \\\\ & \begin{bmatrix}x\\y\\z\end{bmatrix} \begin{bmatrix} m_{11}&m_{12}&m_{13}\\ m_{21}&m_{22}&m_{23}\\ m_{31}&m_{32}&m_{33} \end{bmatrix} = (undefined) \end{align}$$

向量与矩阵中的一些特性如下：

1. 结果向量中的每个元素是原始向量与矩阵中的单个行或列的点积。
2. 矩阵中的每个元素确定输入向量中的特定元素对输出向量中的元素有多大“权重”。如$\mathbf{M_{12}}$就是控制输入的$\mathbf{x}$元素，在输出的$\mathbf{y}$元素上的占比（权重）。所以对输入的向量而言，所有控制输入向量X分量的元素都在第一行，所有控制Y分量的元素都在第二行，所有控制Z分量的元素都在第三行，即矩阵的每一行都代表一个基础向量（类似于X轴，Y轴）。
3. 向量与矩阵乘法分布在向量加法上，即对向量$\mathbf{v、w}$和矩阵$\mathbf{M}$，有$\mathbf{(v+w)M=vM+wM}$。
4. 乘法的结果是矩阵的行或列的线性组合。

¶4.1.8 行与列向量

行向量与列向量本质上并没有区别，但需要注意使用行列向量与矩阵相乘时的顺序是不同的。假设向量$\mathbf{v}$需要与矩阵$\mathbf{A,B,C}$依次相乘。如果$\mathbf{v}$是列向量，那么向量应该出现在右侧，因此转换将从右到左的顺序进行，即写为$\mathbf{CBAv}$。如果$\mathbf{v}$是行向量，那么向量应该出现在左侧，矩阵转换将从左到右的变换顺序列出，即写为$\mathbf{vABC}$。

且行向量与列向量与同一个矩阵相乘后，对应的元素是不同的（如行向量计算结果的第一个元素与列向量计算结果的第一个元素不同）。因此如果想要使用行向量进行计算和使用列向量进行计算的结果向量元素一一对应相等的话，则它们各自使用的矩阵必须是不同的，且为转置关系。

行向量的优点在于，阅读的顺序和相乘的顺序是一致的，即从左到右，而列向量乘积的相乘顺序则是从右到左，但行向量的主要缺点在于，当向量的维度增加时，会让表达式变得非常的长，造成书写的不便，而使用列向量就不会有这个问题。

对于数学家而言，因为需要用到推到，所以他们更喜欢用写起来较短的列向量表达式。而对于计算机而言，因为没有书写的问题，所以更喜欢阅读和相乘顺序相同的行向量，本书也是使用行向量作为与矩阵相乘的向量，之后章节计算出的各种变换矩阵都是基于行向量的，如果要使用在列向量的计算环境下，需要进行转置。

DirectX使用行向量，OpenGL使用列向量。当使用别人的表达式或者代码时，需要特别注意它使用的是行向量还是列向量。

¶4.2 矩阵的几何解释

从几何意义角度来说，方阵可以描述任何的线性变化（Linear transformation）。

线性变化保证了图形中的线条不会被弯曲，且线条们的平行性质不会给改变，但其他的几何性质，如角度，面积，体积，长度都可能发现变化。线性变化包括：

1. 旋转(Rotation)
2. 缩放(Scale)
3. 正交投影(Orthographic projection)
4. 反射(Reflection)
5. 切边（shearing）

已知标准基向量$\textbf{i}=[1,0,0],\textbf{j}=[0,1,0],\textbf{k}=[0,0,1]$，当它们乘以任意矩阵$\mathbf{M}$时：

$$\mathbf{iM}=\begin{bmatrix}1&0&0\end{bmatrix} \begin{bmatrix} m_{11}&m_{12}&m_{13}\\ m_{21}&m_{22}&m_{23}\\ m_{31}&m_{32}&m_{33} \end{bmatrix} = \begin{bmatrix} m_{11}&m_{12}&m_{13} \end{bmatrix} \\ \mathbf{jM}=\begin{bmatrix}1&0&0\end{bmatrix} \begin{bmatrix} m_{11}&m_{12}&m_{13}\\ m_{21}&m_{22}&m_{23}\\ m_{31}&m_{32}&m_{33} \end{bmatrix} = \begin{bmatrix} m_{21}&m_{22}&m_{23} \end{bmatrix} \\ \mathbf{kM}=\begin{bmatrix}1&0&0\end{bmatrix} \begin{bmatrix} m_{11}&m_{12}&m_{13}\\ m_{21}&m_{22}&m_{23}\\ m_{31}&m_{32}&m_{33} \end{bmatrix} = \begin{bmatrix} m_{31}&m_{32}&m_{33} \end{bmatrix}$$

任何向量都可以写成标准基向量的线性组合，如：$\mathbf{v}=v_x\mathbf{i}+v_y\mathbf{k}+v_z\mathbf{k}$。

使用该表达式乘以右侧矩阵，可获得：

$$\begin{align} \mathbf{vM}&=(v_x\mathbf{i}+v_y\mathbf{k}+v_z\mathbf{k})\mathbf{M} \\ &= (v_x\mathbf{i})\mathbf{M}+(v_y\mathbf{k})\mathbf{M}+(v_z\mathbf{k})\mathbf{M} \\ &= v_x(\mathbf{i}\mathbf{M})+v_y(\mathbf{k}\mathbf{M})+v_z(\mathbf{k}\mathbf{M}) \\ &= v_x\begin{bmatrix}m_{11}&m_{12}&m_{13}\end{bmatrix} + v_y\begin{bmatrix}m_{21}&m_{22}&m_{23}\end{bmatrix}+v_z\begin{bmatrix}m_{31}&m_{32}&m_{33}\end{bmatrix} \end{align}$$

可以将矩阵的每一行看作是一个基本向量，即$\begin{bmatrix}m_{11}&m_{12}&m_{13}\end{bmatrix},\begin{bmatrix}m_{21}&m_{22}&m_{23}\end{bmatrix},\begin{bmatrix}m_{31}&m_{32}&m_{33}\end{bmatrix}$都是基本向量，将其命名为$\mathbf{p,q,r}$，则上式结果可以改写为:$\mathbf{vM}=v_x\mathbf{p}+v_y\mathbf{q}+v_z\mathbf{r}$。

可以通过上述的方法来直接判断一个方阵所代表的线性变化，方阵的每一行都是变换后的基本向量，如有$2 \times 2$的矩阵$\mathbf{M}$:

$$\mathbf{M}= \begin{bmatrix} 2&1\\ -1&2 \end{bmatrix}$$

提取基向量$\mathbf{p}$和$\mathbf{q}$:

$$\mathbf{p}=\begin{bmatrix}2&1\end{bmatrix}, \\ \mathbf{q}=\begin{bmatrix}-1&2\end{bmatrix}$$

矩阵可视化如下：

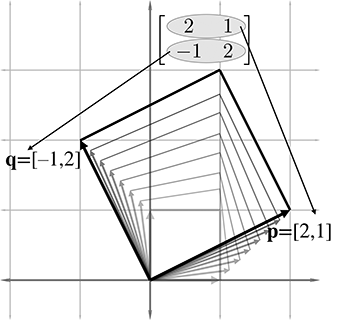
矩阵可视化后，$\mathbf{M}$不仅可以旋转坐标空间，还可以进其缩放，如下图所示：

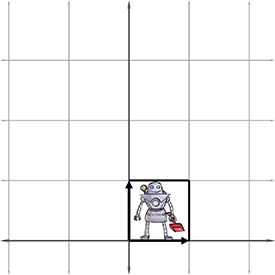
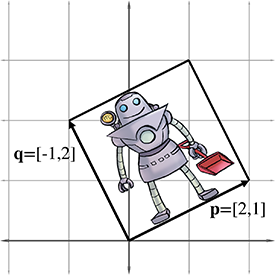
对于三维矩阵同样如此，如有三维矩阵$\begin{bmatrix}0.707&-0.707&0\\1.25&1.25&0\\0&0&1\end{bmatrix}$，将其用于三维模型的坐标变换，则结果如下图所示：

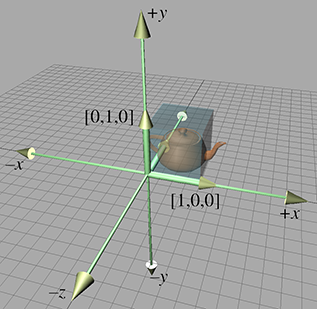
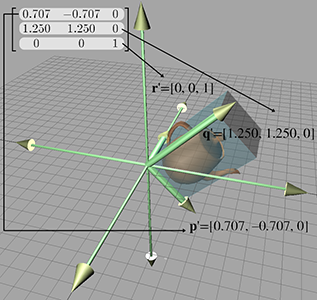
如同可以通过矩阵来直接判断出基本向量的变换，也可以直接通过基本向量的变换来构建出矩阵，只要将对应的基本向量填入每一行即可。

1. 方形矩阵的行可以解释为坐标空间的基向量。
2. 要将向量从原始坐标空间变换到新坐标空间，可以将向量乘以矩阵。
3. 从原始坐标空间到由这些基向量定义的坐标空间的变换是线性变换。线性变换将保留直线，平行线也将保持平行。但是，角度、长度、面积和体积等可能在变换后发生改变。
4. 将零向量乘以任何方形矩阵，得到的是零向量。因此，有方形矩阵表示的线性变换将具有与原始坐标空间相同的原点，这意味着变换不包含平移。
5. 我们可以通过可视化变换后坐标空间的基向量来可视化矩阵。这些基向量在二维中形成L形，而在三维中形成的则是三脚架，使用倾斜框或辅助对象也有助于可视化。

¶4.3 线性代数的宏达图景

线性代数被发明用于操纵和求解线性方程组。

传统线性代数可以求解以下方程组：

$$-5x_1+x_2+x_3=-10,\\ 2x_1+2x_2+4x_3=12,\\ x_1-3x_3=9$$

当用矩阵表达这个方程组时：

$$\begin{bmatrix} -5&1&1\\ 2&2&4\\ 1&0&-3 \end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix} = \begin{bmatrix} -10\\12\\9 \end{bmatrix}$$

---

引用：

1. Dunn, F. and Parberry, I. (2011). 3D math primer for graphics and game development $2^{nd}$.